Calculadora online de arcotangente, es decir, la operación inversa a la tangente que te permitirá conocer el ángulo en grados o radianes asociado a un valor de esta razón trigonométrica.
El funcionamiento de esta calculadora de arcontangente es muy sencillo. Sólo tienes que introducir el valor de la arctan, pulsar el botón de calcular y seleccionar si quieres el resultado en grados (º) o lo prefieres en radianes (rad).
Contenido de este artículo
- ¿Qué es la arcotangente?
- Arcotangente de 1
- Arcotangente de 0
- Arcotangente de infinito
- Gráfica de la función arcotangente
- Tabla de la función arcotangente
- Características de la arcotangente
- Calcular la arcotangente en Excel
- Arcotangente en la calculadora del iPhone
- Cómo usar la calculadora de arcotangente online
¿Qué es la arcotangente?
Como hemos dicho antes, la arcotangente es la función inversa de la tangente:
arctan(y) = tan-1(y) = x+ kπ
Esa es la fórmula matemática o la forma correcta de escribir que vamos a calcular la arctan de un valor concreto. Vamos a verlo con algunos ejemplos a continuación.
Arcotangente de 1
Por ejemplo, sabemos que la tangente de 45º es igual a 1, por lo tanto, al aplicar la arcotangente de 1 obtenemos el ángulo de partida que son esos 45 grados:
arctan(1) = tan-1(1) = 45°
Arcotangente de 0
Ahora vamos a hacer lo mismo que en el ejemplo anterior pero esta vez con el valor cero, una de las preguntas más comunes cuando hablamos de la función arctan. Vamos a calcular la arcotangente en este caso y, posteriormente, analizar el resultado obtenido:
arctan(0) = tan-1(0) = 0°
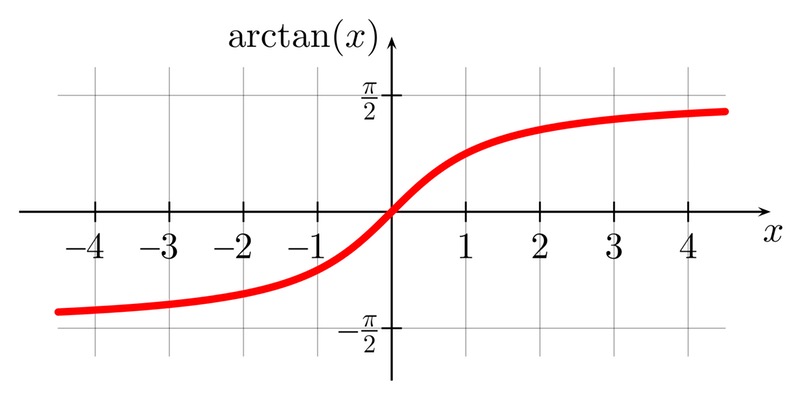
¿Es un resultado esperado? Sí puesto que la tangente de cero también tiene ese valor, es decir, 0. Para que quede más claro lo que estamos diciendo, a continuación tienes un gráfico en el que se puede ver cómo la función pasa por el origen y se verifica esto que acabamos de decir.
Arcotangente de infinito
¿Cuál es la arcotangente de infinito o de menos infinito? En este caso, tenemos que hacer uso de los límites para resolver este problema.
Si queremos calcular la arcotangente de infinito, vemos que el límite es igual a π/2 o 90º:
Si lo que queremos saber es la arcotangente de menos infinito, entonces tenemos el mismo resultado pero con un signo menos.
Gráfica de la función arcotangente
En este gráfico que tenéis justo encima podéis ver la apariencia que tiene la función arcotangente para un intervalo de valores acotado que tiene hacia π/2 y hacia - π/2
Tabla de la función arcotangente
A continuación tienes una tabla de arcotangente que recoge los valores más utilizados en problemas de trigonometría o en aquellos que involucre a esta función trigonométrica:
| y | x = arctan(y) en grados | x = arctan(y) en radianes |
|---|---|---|
| -1,732050808 | -60° | -π/3 |
| -1 | -45° | -π/4 |
| -0,577350269 | -30° | -π/6 |
| 0 | 0° | 0 |
| 0,577350269 | 30° | π/6 |
| 1 | 45° | π/4 |
| 1,732050808 | 60° | π/3 |
Características de la arcotangente
Terminamos la sección dedicada a esta función trigonométrica hablando un poco de las propiedades de la arcotangente, incluyendo su dominio, recorrido, derivada y la integral.
Dominio
La función arctan(y) tiene un dominio que va desde menos infinito hasta más infinito, no hay ningún corte en ese intervalo. Por lo tanto, podemos decir que están incluidos todos los números reales:
arctan(y) :[-∞ , +∞]
Esto se puede apreciar en la gráfica que tenéis más arriba.
Recorrido
En este caso, y podemos comprobarlo en la gráfica, el recorrido va desde [- π/2 , π/2]
Debido a las dos propiedades anteriores, podemos decir que la función arcotangente es continua y creciente en todo R.
Derivada arcotangente
Esta es la fórmula que obtenemos al calcular la derivada de la arctan x:
Si en lugar de x tenemos una función u, entonces se puede decir que la derivada de arcotangente de una función es igual a la derivada de dicha función dividida entre uno más la función elevada al cuadrado. Esto queda expresado de la siguiente manera:
Integral
Por último, esta es la integral obtenida para la función:
Calcular la arcotangente en Excel
Excel incorpora una función que te permite calcular la arcotangente de forma directa y sin cálculos. Simplemente tienes que abrir una nueva hoja de cálculo y escribir la siguiente fórmula en una celda vacía:
=ATAN()
Debes tener en cuenta que entre los paréntesis debes escribir el valor del número para el cual quieres obtener su arcotangente, además, el resultado que da Excel por defecto vendrá expresado en radianes en el rango que va cubre [- π/2 , π/2].
Como ejemplo práctico, vamos a calcular la arcotangente de 2 en Exscel,
=ATAN(2)
Eso nos dará un resultado de 1,107148718 radianes pero si queremos expresarlo en grados, tendremos que escribir la fórmula de la siguiente forma:
=GRADOS(ATAN(2))
Lo que nos dará un resultado de 63,43494882 grados para la arcotangente de 2. Dependiendo de la unidad que necesites, tendrás que usar una u otra fórmula de Excel para sacar la arcotangente de un número.
Arcotangente en la calculadora del iPhone
La calculadora del iPhone permite hacer la ATAN (inversa de la tangente) pero tiene un método poco intuitivo, por lo que quizás no sepas cómo se hace.
Para ello, lo primero que debes hacer es desactivar el bloqueo de rotación de la pantalla si es que lo tenías activado. A continuación entra en la aplicación de la calculadora, gira el móvil 90º para ponerlo en modo horizontal y tendrás acceso a la versión científica de la app.
Ahora, pulsa ese botón que pone 2nd, escribe el número para el cual quieres saber su arcotangente y cuando lo hayas hecho, pulsa la tecla en la que está escrito "tan-1".
Cómo usar la calculadora de arcotangente online
Calcular la arcotangente online es algo que muchos queréis para no tener que usar la calculadora, por eso, hemos grabado un vídeo en el que te explicamos cómo se utiliza nuestra calculadora para que no tengas ninguna duda del proceso a seguir.
Lo único que debes tener en cuenta es que de cara a calcular la arctag de un número decimal, debes usar como separador un . en lugar de la coma (,) ya que de lo contrario, sólo cogerá la parte entera y el ángulo resultante no será el que realmente estás buscando.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.

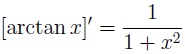
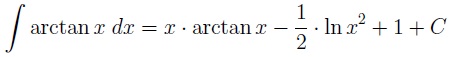

me encanta esta página, me ayudó mucho ..gracias
Hola Lola,
Muchas gracias por tu comentario. Si necesitas cualquier ayuda para resolver la arcotangente o cualquier otra razón trigonométrica no dudes en preguntarnos, vale?
Un saludo!
arctg de un medio porffaaa
Hola Jhafer,
La arcotangente de 0,5 es = tan⁻¹ 0.5 = 26º 33′ 54.184″ = 26.56505118º+k×180º (k=..-1,0,1,..) = -153.43494882º, 26.56505118º, 206.56505118º, .. = 0.46364761rad+k×π (k=..-1,0,1,..) = -0.85241638π, 0.14758362π, 1.14758362π,
Un saludo!
¡Muy buena herramienta!, la compartiré…., ¡ Muchas Gracias!