Deprecated: Creation of dynamic property wpdb::$categories is deprecated in /home/calculadsa/www/wp-includes/wp-db.php on line 760

Deprecated: Creation of dynamic property wpdb::$post2cat is deprecated in /home/calculadsa/www/wp-includes/wp-db.php on line 760

Deprecated: Creation of dynamic property wpdb::$link2cat is deprecated in /home/calculadsa/www/wp-includes/wp-db.php on line 760

Deprecated: Using ${var} in strings is deprecated, use {$var} instead in /home/calculadsa/www/wp-includes/comment-template.php on line 1745

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Return type of Pimple\Container::offsetExists($id) should either be compatible with ArrayAccess::offsetExists(mixed $offset): bool, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/vendor-prod/pimple/pimple/src/Pimple/Container.php on line 133

Deprecated: Return type of Pimple\Container::offsetGet($id) should either be compatible with ArrayAccess::offsetGet(mixed $offset): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/vendor-prod/pimple/pimple/src/Pimple/Container.php on line 98

Deprecated: Return type of Pimple\Container::offsetSet($id, $value) should either be compatible with ArrayAccess::offsetSet(mixed $offset, mixed $value): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/vendor-prod/pimple/pimple/src/Pimple/Container.php on line 79

Deprecated: Return type of Pimple\Container::offsetUnset($id) should either be compatible with ArrayAccess::offsetUnset(mixed $offset): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/vendor-prod/pimple/pimple/src/Pimple/Container.php on line 143

Deprecated: Return type of iThemesSecurity\Lib\Lockout\Execute_Lock\Context::offsetExists($offset) should either be compatible with ArrayAccess::offsetExists(mixed $offset): bool, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/lockout/execute-lock/abstract-context.php on line 60

Deprecated: Return type of iThemesSecurity\Lib\Lockout\Execute_Lock\Context::offsetGet($offset) should either be compatible with ArrayAccess::offsetGet(mixed $offset): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/lockout/execute-lock/abstract-context.php on line 66

Deprecated: Return type of iThemesSecurity\Lib\Lockout\Execute_Lock\Context::offsetSet($offset, $value) should either be compatible with ArrayAccess::offsetSet(mixed $offset, mixed $value): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/lockout/execute-lock/abstract-context.php on line 72

Deprecated: Return type of iThemesSecurity\Lib\Lockout\Execute_Lock\Context::offsetUnset($offset) should either be compatible with ArrayAccess::offsetUnset(mixed $offset): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/lockout/execute-lock/abstract-context.php on line 76

Deprecated: Return type of iThemesSecurity\Lib\Lockout\Execute_Lock\Context::getIterator() should either be compatible with IteratorAggregate::getIterator(): Traversable, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/lockout/execute-lock/abstract-context.php on line 56

Deprecated: Return type of ITSEC_Lib_Distributed_Storage_Cursor::current() should either be compatible with Iterator::current(): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/class-itsec-lib-distributed-storage.php on line 578

Deprecated: Return type of ITSEC_Lib_Distributed_Storage_Cursor::next() should either be compatible with Iterator::next(): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/class-itsec-lib-distributed-storage.php on line 585

Deprecated: Return type of ITSEC_Lib_Distributed_Storage_Cursor::key() should either be compatible with Iterator::key(): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/class-itsec-lib-distributed-storage.php on line 606

Deprecated: Return type of ITSEC_Lib_Distributed_Storage_Cursor::valid() should either be compatible with Iterator::valid(): bool, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/class-itsec-lib-distributed-storage.php on line 613

Deprecated: Return type of ITSEC_Lib_Distributed_Storage_Cursor::rewind() should either be compatible with Iterator::rewind(): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/class-itsec-lib-distributed-storage.php on line 620

Deprecated: Using ${var} in strings is deprecated, use {$var} instead in /home/calculadsa/www/wp-content/plugins/contact-form-7/includes/mail.php on line 221

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Return type of WPGMZA\CustomFeatureFields::getIterator() should either be compatible with IteratorAggregate::getIterator(): Traversable, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-map-object-fields.php on line 120

Deprecated: Return type of WPGMZA\CustomFeatureFields::jsonSerialize() should either be compatible with JsonSerializable::jsonSerialize(): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-map-object-fields.php on line 129

Deprecated: Return type of WPGMZA\CustomFeatureFields::count() should either be compatible with Countable::count(): int, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-map-object-fields.php on line 111

Deprecated: Return type of WPGMZA\CustomFields::getIterator() should either be compatible with IteratorAggregate::getIterator(): Traversable, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-fields.php on line 121

Deprecated: Return type of WPGMZA\CustomFields::jsonSerialize() should either be compatible with JsonSerializable::jsonSerialize(): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-fields.php on line 130

Deprecated: Return type of WPGMZA\CustomFields::count() should either be compatible with Countable::count(): int, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-fields.php on line 136

Deprecated: Using ${var} in strings is deprecated, use {$var} instead in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/modules/core/class-itsec-admin-notices.php on line 141

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property WPGMZA\ProDatabase::$version is deprecated in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/class.pro-database.php on line 12

Deprecated: Creation of dynamic property WPGMZA\ProDatabase::$charset_collate is deprecated in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/class.pro-database.php on line 13

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property WP_Rocket\Engine\Preload\SitemapPreloadSubscriber::$options is deprecated in /home/calculadsa/www/wp-content/plugins/wp-rocket/inc/Engine/Preload/SitemapPreloadSubscriber.php on line 26

Deprecated: Creation of dynamic property WP_Rocket\Engine\Preload\SitemapPreloadSubscriber::$sitemap_preload is deprecated in /home/calculadsa/www/wp-content/plugins/wp-rocket/inc/Engine/Preload/SitemapPreloadSubscriber.php on line 27

Deprecated: Automatic conversion of false to array is deprecated in /home/calculadsa/www/wp-content/plugins/wp-rocket/inc/3rd-party/plugins/seo/yoast-seo.php on line 10

Deprecated: Creation of dynamic property Yoast\WP\SEO\Main::$helpers is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/lib/abstract-main.php on line 65

Deprecated: trim(): Passing null to parameter #1 ($string) of type string is deprecated in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/core.php on line 1092

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property WP_Block_Type::$skip_inner_blocks is deprecated in /home/calculadsa/www/wp-includes/class-wp-block-type.php on line 357

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Constant FILTER_SANITIZE_STRING is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/conditionals/third-party/elementor-edit-conditional.php on line 22

Deprecated: Constant FILTER_SANITIZE_STRING is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/conditionals/third-party/elementor-edit-conditional.php on line 28

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property Yoast\WP\SEO\Surfaces\Classes_Surface::$container is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/surfaces/classes-surface.php on line 20

Deprecated: Creation of dynamic property Yoast\WP\SEO\Main::$classes is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/lib/abstract-main.php on line 65

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$page_type is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 43

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$robots is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$title is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$source is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64
Calculadora del área de una pirámide - Fórmula y ejercicios ▲
Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$meta_description is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$canonical is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$rel_prev is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$rel_next is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_locale is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_type is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_title is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_description is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_url is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$wordpress_site_name is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_site_name is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$company_name is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$company_logo_id is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$site_represents is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$open_graph_publisher is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_article_publisher is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_article_author is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_article_published_time is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_article_modified_time is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$open_graph_enabled is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_images is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$twitter_card is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_card is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_title is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_description is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_image is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_creator is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_site is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$estimated_reading_time_minutes is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$canonical is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$main_schema_id is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$site_url is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$schema_article_type is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$company_logo_meta is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$site_name is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$site_represents_reference is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$id is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$main_image_id is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$schema_page_type is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$title is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$main_image_url is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$has_image is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$description is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$breadcrumbs is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: strtolower(): Passing null to parameter #1 ($string) of type string is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/generators/schema-generator.php on line 176

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$schema is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Área de una pirámide

Resumen

Calcula el área de una pirámide online y descubre cómo sacar la superficie de una pirámide con su fórmula. Ejercicios resueltos incluidos.

¿Quieres calcular el área de una pirámide? Usa nuestra calculadora online y te proporcionaremos automáticamente datos como la superficie lateral de esta figura, el área de su base y la superficie total que tenga esa pirámide.

Sólo tienes que introducir cuánto mide uno de los lados de la base cuadrangular y la altura que tiene la pirámide. Cuando lo hayas hecho, pulsa el botón de calcular y te daremos los resultados.


Cómo calcular el área de una pirámide

Tipos de pirámides

Para calcular el área de una pirámide tenemos que seguir tres pasos:

  1. Sacar su superficie lateral
  2. Obtener la superficie que ocupa la base cuadrangular
  3. Sumar los resultados obtenidos en los dos puntos anteriores.

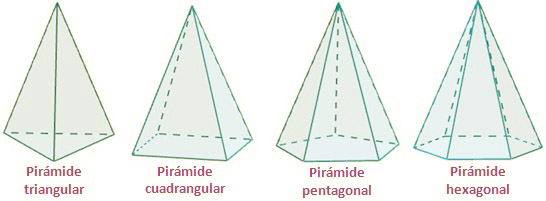
Vamos a ver cómo se hace cada uno para que no haya ninguna duda. Presta atención porque dependiendo del tipo de pirámide que tengamos (triangular, cuadrangular, pentagonal, hexágonal...), habrá que usar la fórmula de una forma u otra.

Área lateral de una pirámide

El primer paso para calcular el área de una pirámide consiste en hallar su superficie lateral. Para ello aplicaremos la siguiente fórmula:

Área lateral pirámide = base x altura x N / 2

Siendo N el número de lados que tiene la base. Por ejemplo, en el caso de una pirámide triangular N es 3, en la cuadrangular será N= 4, en la pentagonal N = 5 y así sucesivamente.

Ten en cuenta que el número de lados de la base influye directamente en el número de caras que tendrá la pirámide. Por ejemplo, en el caso de una pirámide hexagonal estamos hablando de 6 caras.

Superficie de la base

Calculadora Área pirámide

Para calcular la superficie de la base de la pirámide tenemos que usar la fórmula que corresponda al polígono que hay en la parte inferior.

Por ejemplo, si la base es triangular la fórmula es

A = base x altura /2

Pero si la pirámide es cuadrangular, la superficie de la base la calcularemos con esta otra:

A = lado x lado

Si necesitas conocer el área de algún otro tipo de base, déjanos un comentario y te ayudaremos lo antes posible.

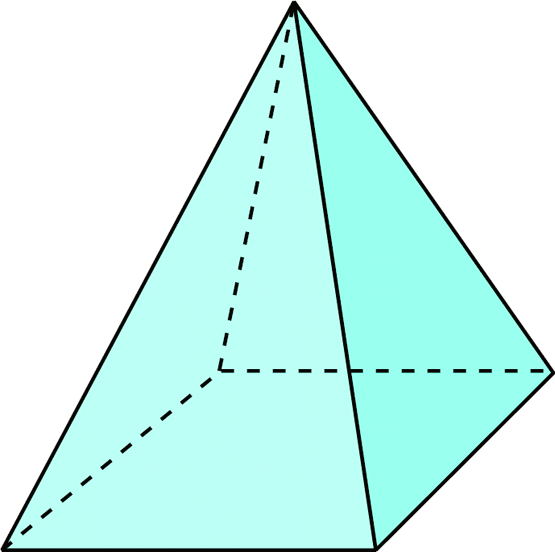
Ejercicio resuelto: pirámide cuadrangular

Pirámide cuadrangular

Nos piden hallar el área de una pirámide cuadrangular cuya altura es de 12 metros y el lado de la base es de 4 metros.

Siguiendo los pasos que hemos visto en el punto de teoría, lo primero que haremos será sacar el área de la superficie total. Como estamos ante una pirámide con base cuadrada, el número de lados será cuatro (N = 4)

Área lateral pirámide = 4 x 12 x 4 / 2 = 96 m2

Ahora calculamos el área de la base:

Área base pirámide = 4 x 4 = 16 m2

Sumamos todas las áreas:

Área pirámide = 96m2 + 16m2 = 112 m2

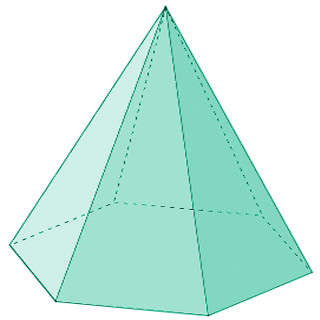
Ejemplo: pirámide hexagonal

Pirámide hexagonal

Vamos a ver otro ejemplo práctico pero esta vez nos piden hallar la superficie de una pirámide hexagonal con 10 metros de altura y cuyos lados de la base miden 5 metros.

Volvemos a poner en práctica el método de resolución anterior, así que lo primero que haremos será calcular el área lateral. En este caso se trata de una pirámide cuya base es un hexágono por lo que tenemos 6 caras:

Área lateral pirámide = 4 x 10 x 6 / 2 = 120 m2

Hallamos la superficie de la base hexagonal cuya fórmula sin saber la apotema es:

Área hexágono = 2,60 · L2 = 2,60 · 52 = 65 m2

Sumamos y obtenemos el área total de la pirámide hexagonal:

Superficie pirámide hexagonal = 120 m2 + 65 m2 = 185 m2


Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property WP_Term::$cat_ID is deprecated in /home/calculadsa/www/wp-includes/category.php on line 378

Deprecated: Creation of dynamic property WP_Term::$category_count is deprecated in /home/calculadsa/www/wp-includes/category.php on line 379

Deprecated: Creation of dynamic property WP_Term::$category_description is deprecated in /home/calculadsa/www/wp-includes/category.php on line 380

Deprecated: Creation of dynamic property WP_Term::$cat_name is deprecated in /home/calculadsa/www/wp-includes/category.php on line 381

Deprecated: Creation of dynamic property WP_Term::$category_nicename is deprecated in /home/calculadsa/www/wp-includes/category.php on line 382

Deprecated: Creation of dynamic property WP_Term::$category_parent is deprecated in /home/calculadsa/www/wp-includes/category.php on line 383

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$cat_ID is deprecated in /home/calculadsa/www/wp-includes/category.php on line 378

Deprecated: Creation of dynamic property WP_Term::$category_count is deprecated in /home/calculadsa/www/wp-includes/category.php on line 379

Deprecated: Creation of dynamic property WP_Term::$category_description is deprecated in /home/calculadsa/www/wp-includes/category.php on line 380

Deprecated: Creation of dynamic property WP_Term::$cat_name is deprecated in /home/calculadsa/www/wp-includes/category.php on line 381

Deprecated: Creation of dynamic property WP_Term::$category_nicename is deprecated in /home/calculadsa/www/wp-includes/category.php on line 382

Deprecated: Creation of dynamic property WP_Term::$category_parent is deprecated in /home/calculadsa/www/wp-includes/category.php on line 383

Calculadora Conversor > Calculadoras matemáticas > Áreas de figuras geométricas > Área de una pirámide

Otras calculadoras y conversores que te pueden interesar:


Deprecated: Creation of dynamic property WP_Query::$comments_by_type is deprecated in /home/calculadsa/www/wp-includes/comment-template.php on line 1528

4 comentarios en «Área de una pirámide»

    • Al contrario, tienes ejemplos para calcular el área de una pirámide cuya base puede ser triangular, cuadrangular, pentagonal o incluso hexagonal. Te recomiendo que revises el contenido que tenemos para comprobarlo ;)

  3. Buena para diseñar y elaborar una pirámide tridimensional que puede descomponerse en dos figuras conocidas. Dibújala y Explica cómo lo harías

    Responder

Deja un comentario

Información sobre protección de datos

  • Responsable: Ignacio Cuesta
  • Fin del tratamiento: Controlar el spam, gestión de comentarios
  • Legitimación: Tu consentimiento
  • Comunicación de los datos: No se comunicarán los datos a terceros salvo por obligación legal.
  • Derechos: Acceso, rectificación, portabilidad, olvido.
  • Contacto: contacto@calculadoraconversor.com.
  • Información adicional: Más información en nuestra política de privacidad.


Deprecated: Creation of dynamic property WP_Term::$cat_ID is deprecated in /home/calculadsa/www/wp-includes/category.php on line 378

Deprecated: Creation of dynamic property WP_Term::$category_count is deprecated in /home/calculadsa/www/wp-includes/category.php on line 379

Deprecated: Creation of dynamic property WP_Term::$category_description is deprecated in /home/calculadsa/www/wp-includes/category.php on line 380

Deprecated: Creation of dynamic property WP_Term::$cat_name is deprecated in /home/calculadsa/www/wp-includes/category.php on line 381

Deprecated: Creation of dynamic property WP_Term::$category_nicename is deprecated in /home/calculadsa/www/wp-includes/category.php on line 382

Deprecated: Creation of dynamic property WP_Term::$category_parent is deprecated in /home/calculadsa/www/wp-includes/category.php on line 383

Deprecated: Use of "parent" in callables is deprecated in /home/calculadsa/www/wp-content/plugins/wp-rocket/inc/Dependencies/Minify/JS.php on line 127