¿Necesitas calcular el tamaño muestral? Usa nuestra calculadora online y podrás conseguir el tamaño de la muestra adecuado para la población que quieres investigar.
Para usar la calculadora de tamaño muestral sólo necesitas rellenar cuatro datos imprescindibles: el tamaño de la población, el porcentaje de desviación, el porcentaje de error máximo que admites y el nivel de confianza. Si no sabes qué son estos parámetros, sigue leyendo para entender bien cómo se calcula el tamaño de una muestra.
Contenido de este artículo
Datos para calcular el tamaño muestral
Para poder calcular el tamaño muestral hay que conocer una serie de factores que os contamos a continuación:
- Margen de error: se define como el rango en el que deseamos encontrar el dato a analizar dentro de la población. El margen de error suele representar una media o una proporción. Ten en cuenta que si reduces el margen de error, tenemos que aumentar el tamaño de la muestra para que el resultado sea fiable. A su vez, si aumentamos el tamaño de la muestra podemos reducir el margen de error o aumenta el nivel de confianza.
- Nivel de confianza: este dato viene a representar la seguridad que tenemos de que el dato que queremos esté dentro del margen de error.
- Población: es el grupo de elementos que comparten una característica común (por ejemplo, los habitantes de una misma ciudad). La población puede ser finita o infinita. Una población finita es aquella que está delimitada y conocemos cuántos miembros la forman mientras que una población infinita es aquella que está delimitada pero no sabemos cuántos miembros hay en ella.
- Desviación estándar: si no conocemos su valor usaremos un 50%.
Con todos estos datos, podremos calcular el tamaño muestral a partir de la fórmula que veremos en el siguiente punto.
Fórmula para calcular una muestra representativa
Esta es la fórmula que debes aplicar para calcular el tamaño muestral:
Siendo:
- N el tamaño de la población o universo
- e es el margen de error
- p es la proporción que queremos encontrar y que se corresponde con el valor de la desviación estándar que vimos en el apartado anterior. Si no conocemos su valor, usaremos un 50%, es decir, 0,5 en la fórmula.
- Z es una constante que depende del nivel de confianza y cuyos valores se sacan de la tabla de la distribución normal estándar N(0,1). A continuación os dejamos los valores de Z más utilizados en función de su nivel de confianza:
| Nivel de confianza | Valor de Z |
|---|---|
| 75% | 1.15 |
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 97,5% | 2.24 |
| 99% | 2.58 |
Si el tamaño de la población es muy grande (más de 100.000 elementos), la fórmula anterior se puede simplificar y quedaría así:
Ejemplo resuelto para calcular tamaño de la muestra
Vamos a ver un ejercicio resuelto en el que nos piden calcular el tamaño de la muestra para una ciudad cuya población es de 80.000 habitantes y queremos saber el porcentaje de ellos que viven de alquiler, con un margen de error del 5% y un nivel de confianza del 95% (Z = 1,64)
Como el tamaño de la población es menor de 100.000, usaremos la fórmula completa para calcular el tamaño de la muestra:
n = [80.000 x 1,642 x 0,5 x (1 - 0,5)] / [(80.000 - 1) x 0,52 + 1,642 x 0,5 x (1 - 0,5)] = 383
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.

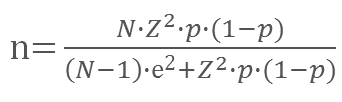
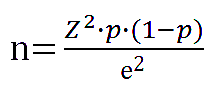
muy interesante,y gracias por la simplificación operativa
Hola Ulises,
Muchas gracias por dedicar un rato de tu tiempo a dejarnos ese comentario. Nos alegra que te haya gustado.
Saludos!
Excelentes datos.
gracias me ayudo mucho tu forma de simplificar los cálculos
saludos