Deprecated: Creation of dynamic property wpdb::$categories is deprecated in /home/calculadsa/www/wp-includes/wp-db.php on line 760

Deprecated: Creation of dynamic property wpdb::$post2cat is deprecated in /home/calculadsa/www/wp-includes/wp-db.php on line 760

Deprecated: Creation of dynamic property wpdb::$link2cat is deprecated in /home/calculadsa/www/wp-includes/wp-db.php on line 760

Deprecated: Using ${var} in strings is deprecated, use {$var} instead in /home/calculadsa/www/wp-includes/comment-template.php on line 1745

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Return type of Pimple\Container::offsetExists($id) should either be compatible with ArrayAccess::offsetExists(mixed $offset): bool, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/vendor-prod/pimple/pimple/src/Pimple/Container.php on line 133

Deprecated: Return type of Pimple\Container::offsetGet($id) should either be compatible with ArrayAccess::offsetGet(mixed $offset): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/vendor-prod/pimple/pimple/src/Pimple/Container.php on line 98

Deprecated: Return type of Pimple\Container::offsetSet($id, $value) should either be compatible with ArrayAccess::offsetSet(mixed $offset, mixed $value): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/vendor-prod/pimple/pimple/src/Pimple/Container.php on line 79

Deprecated: Return type of Pimple\Container::offsetUnset($id) should either be compatible with ArrayAccess::offsetUnset(mixed $offset): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/vendor-prod/pimple/pimple/src/Pimple/Container.php on line 143

Deprecated: Return type of iThemesSecurity\Lib\Lockout\Execute_Lock\Context::offsetExists($offset) should either be compatible with ArrayAccess::offsetExists(mixed $offset): bool, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/lockout/execute-lock/abstract-context.php on line 60

Deprecated: Return type of iThemesSecurity\Lib\Lockout\Execute_Lock\Context::offsetGet($offset) should either be compatible with ArrayAccess::offsetGet(mixed $offset): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/lockout/execute-lock/abstract-context.php on line 66

Deprecated: Return type of iThemesSecurity\Lib\Lockout\Execute_Lock\Context::offsetSet($offset, $value) should either be compatible with ArrayAccess::offsetSet(mixed $offset, mixed $value): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/lockout/execute-lock/abstract-context.php on line 72

Deprecated: Return type of iThemesSecurity\Lib\Lockout\Execute_Lock\Context::offsetUnset($offset) should either be compatible with ArrayAccess::offsetUnset(mixed $offset): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/lockout/execute-lock/abstract-context.php on line 76

Deprecated: Return type of iThemesSecurity\Lib\Lockout\Execute_Lock\Context::getIterator() should either be compatible with IteratorAggregate::getIterator(): Traversable, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/lockout/execute-lock/abstract-context.php on line 56

Deprecated: Return type of ITSEC_Lib_Distributed_Storage_Cursor::current() should either be compatible with Iterator::current(): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/class-itsec-lib-distributed-storage.php on line 578

Deprecated: Return type of ITSEC_Lib_Distributed_Storage_Cursor::next() should either be compatible with Iterator::next(): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/class-itsec-lib-distributed-storage.php on line 585

Deprecated: Return type of ITSEC_Lib_Distributed_Storage_Cursor::key() should either be compatible with Iterator::key(): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/class-itsec-lib-distributed-storage.php on line 606

Deprecated: Return type of ITSEC_Lib_Distributed_Storage_Cursor::valid() should either be compatible with Iterator::valid(): bool, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/class-itsec-lib-distributed-storage.php on line 613

Deprecated: Return type of ITSEC_Lib_Distributed_Storage_Cursor::rewind() should either be compatible with Iterator::rewind(): void, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/lib/class-itsec-lib-distributed-storage.php on line 620

Deprecated: Using ${var} in strings is deprecated, use {$var} instead in /home/calculadsa/www/wp-content/plugins/contact-form-7/includes/mail.php on line 221

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Return type of WPGMZA\CustomFeatureFields::getIterator() should either be compatible with IteratorAggregate::getIterator(): Traversable, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-map-object-fields.php on line 120

Deprecated: Return type of WPGMZA\CustomFeatureFields::jsonSerialize() should either be compatible with JsonSerializable::jsonSerialize(): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-map-object-fields.php on line 129

Deprecated: Return type of WPGMZA\CustomFeatureFields::count() should either be compatible with Countable::count(): int, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-map-object-fields.php on line 111

Deprecated: Return type of WPGMZA\CustomFields::getIterator() should either be compatible with IteratorAggregate::getIterator(): Traversable, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-fields.php on line 121

Deprecated: Return type of WPGMZA\CustomFields::jsonSerialize() should either be compatible with JsonSerializable::jsonSerialize(): mixed, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-fields.php on line 130

Deprecated: Return type of WPGMZA\CustomFields::count() should either be compatible with Countable::count(): int, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/custom-fields/class.custom-fields.php on line 136

Deprecated: Using ${var} in strings is deprecated, use {$var} instead in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/modules/core/class-itsec-admin-notices.php on line 141

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property WPGMZA\ProDatabase::$version is deprecated in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/class.pro-database.php on line 12

Deprecated: Creation of dynamic property WPGMZA\ProDatabase::$charset_collate is deprecated in /home/calculadsa/www/wp-content/plugins/wp-google-maps-pro/includes/class.pro-database.php on line 13

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property WP_Rocket\Engine\Preload\SitemapPreloadSubscriber::$options is deprecated in /home/calculadsa/www/wp-content/plugins/wp-rocket/inc/Engine/Preload/SitemapPreloadSubscriber.php on line 26

Deprecated: Creation of dynamic property WP_Rocket\Engine\Preload\SitemapPreloadSubscriber::$sitemap_preload is deprecated in /home/calculadsa/www/wp-content/plugins/wp-rocket/inc/Engine/Preload/SitemapPreloadSubscriber.php on line 27

Deprecated: Automatic conversion of false to array is deprecated in /home/calculadsa/www/wp-content/plugins/wp-rocket/inc/3rd-party/plugins/seo/yoast-seo.php on line 10

Deprecated: Creation of dynamic property Yoast\WP\SEO\Main::$helpers is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/lib/abstract-main.php on line 65

Deprecated: trim(): Passing null to parameter #1 ($string) of type string is deprecated in /home/calculadsa/www/wp-content/plugins/better-wp-security/core/core.php on line 1092

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property WP_Block_Type::$skip_inner_blocks is deprecated in /home/calculadsa/www/wp-includes/class-wp-block-type.php on line 357

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Constant FILTER_SANITIZE_STRING is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/conditionals/third-party/elementor-edit-conditional.php on line 22

Deprecated: Constant FILTER_SANITIZE_STRING is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/conditionals/third-party/elementor-edit-conditional.php on line 28

Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property Yoast\WP\SEO\Surfaces\Classes_Surface::$container is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/surfaces/classes-surface.php on line 20

Deprecated: Creation of dynamic property Yoast\WP\SEO\Main::$classes is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/lib/abstract-main.php on line 65

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$page_type is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 43

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$robots is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$title is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$source is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64
Calculadora de valor absoluto online: propiedades y definición
Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$meta_description is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$canonical is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$rel_prev is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$rel_next is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_locale is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_type is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_title is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_description is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_url is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$wordpress_site_name is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_site_name is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$company_name is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$company_logo_id is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$site_represents is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$open_graph_publisher is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_article_publisher is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_article_author is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_article_published_time is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_article_modified_time is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$open_graph_enabled is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$open_graph_images is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$twitter_card is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_card is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_title is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_description is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_image is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_creator is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$twitter_site is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$estimated_reading_time_minutes is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$canonical is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$main_schema_id is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$site_url is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$schema_article_type is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$company_logo_meta is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$site_name is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$site_represents_reference is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$id is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$main_image_id is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$schema_page_type is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$title is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$main_image_url is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$has_image is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Context\Meta_Tags_Context::$description is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$breadcrumbs is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Deprecated: strtolower(): Passing null to parameter #1 ($string) of type string is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/generators/schema-generator.php on line 176

Deprecated: Creation of dynamic property Yoast\WP\SEO\Presentations\Indexable_Post_Type_Presentation::$schema is deprecated in /home/calculadsa/www/wp-content/plugins/wordpress-seo/src/presentations/abstract-presentation.php on line 64

Calculadora de valor absoluto

Resumen

Calcula el valor absoluto de cualquier número online con nuestra calculadora y descubre las propiedades y definición de esta función matemática.

¿Necesitas calcular el valor absoluto de un número? No te preocupes, tenemos para ti una herramienta que te permitirá calcular el resultado de esta función tan utilizada en matemáticas.

Sólo necesitas introducir el número del cual deseas conocer su valor absoluto y pulsar el botón de calcular para obtener el resultado que estás buscando.

¿Qué es el valor absoluto de un número?

Calcular valor absoluto

El valor absoluto o módulo de un número real es otro número cuyo valor se corresponde con su valor numérico sin tener en cuenta su signo, independientemente de que el número sea positivo o negativo.

Para denotar la función de valor absoluto o módulo, se introduce al número entre barras de la siguiente forma: |-3| = 3.

En base a lo anterior, podemos definir que el valor absoluto para un número entero, racional o real será:

  • |a| = a si el número 'a' es mayor o igual que cero (a ≥ 0).
  • |-a| = a si el número 'a' es negativo

Por ejemplo, vamos a calcular el valor absoluto del número 5 y el de -5:

  • |5| = 5
  • |-5| = 5

Como puedes ver, en ambos casos tenemos como resultado del valor absoluto el valor numérico de la cantidad, con independencia de su signo. En definitiva, podemos decir que la función del valor absoluto, abs (x) =|x|, queda definida de la siguiente forma:

  • x, si x ≥ 0
  • -x, si x ≤ 0

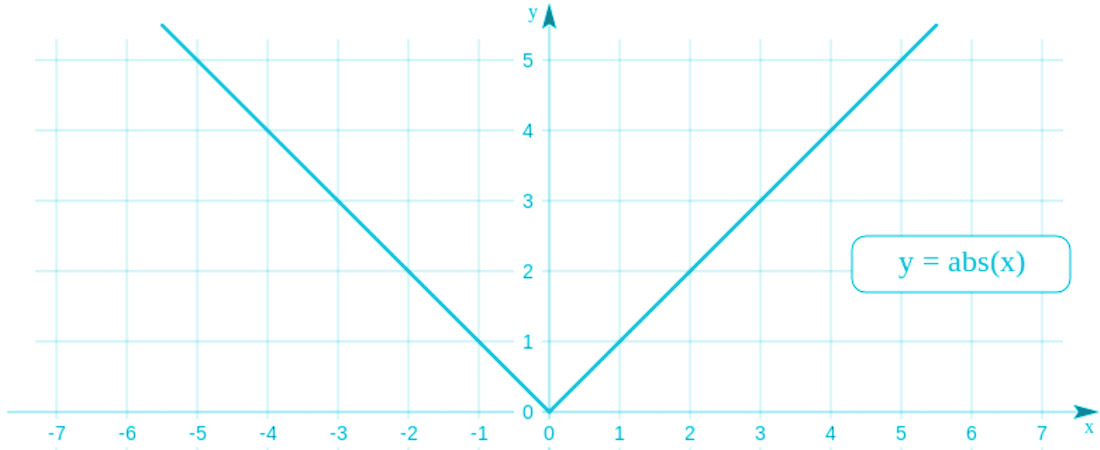
Si esto lo representamos en una gráfica, obtendremos algo como esto:

Gráfica del valor absoluto

En la gráfica del valor absoluto se puede ver con mucha más claridad las propiedades que veremos en el siguiente apartado. Por ejemplo, nunca puede ser negativo y siempre tomará valores mayores o igual a cero.

Propiedades del valor absoluto

A continuación tienes algunas de las principales propiedades asociadas al módulo de un número:

Los números opuestos tienen el mismo valor absoluto

Como has podido comprobar en el ejemplo anterior, el módulo de |a| = |-a|.

Vamos a verlo con otros ejemplos:

  • |4| = |-4|
  • |6| = |-6|
  • |8| = |-8|

El valor absoluto de un producto

Si tienes un valor absoluto de un producto, entonces el resultado puede interpretarse como el producto de los valores absolutos de cada uno de los factores. Esto queda representado de la siguiente forma:

  • |a · b| = |a| · |b|

Veamos lo mismo con un ejemplo práctico:

  • |-3 · 2| = |-3| · |2| = 6

El módulo de una suma

Si tienes el módulo de una suma, el resultado será menor o igual a la suma del módulo de cada uno de los sumandos, es decir:

  • |a + b| ≤ |a| + |b|

Veámoslo con un ejemplo para despejar dudas:

  • |3 + (-4)| ≤ |3| + |(-4)|
    |-1| ≤ |3| + |4|
    1 ≤ 7

Si te ha quedado alguna duda en relación a la función abs(x), déjanos un comentario y te ayudaremos a despejar todas tus dudas.


Deprecated: Creation of dynamic property POMO_FileReader::$is_overloaded is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 26

Deprecated: Creation of dynamic property POMO_FileReader::$_pos is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 29

Deprecated: Creation of dynamic property POMO_FileReader::$_f is deprecated in /home/calculadsa/www/wp-includes/pomo/streams.php on line 160

Deprecated: Creation of dynamic property MO::$_gettext_select_plural_form is deprecated in /home/calculadsa/www/wp-includes/pomo/translations.php on line 293

Deprecated: Creation of dynamic property WP_Term::$cat_ID is deprecated in /home/calculadsa/www/wp-includes/category.php on line 378

Deprecated: Creation of dynamic property WP_Term::$category_count is deprecated in /home/calculadsa/www/wp-includes/category.php on line 379

Deprecated: Creation of dynamic property WP_Term::$category_description is deprecated in /home/calculadsa/www/wp-includes/category.php on line 380

Deprecated: Creation of dynamic property WP_Term::$cat_name is deprecated in /home/calculadsa/www/wp-includes/category.php on line 381

Deprecated: Creation of dynamic property WP_Term::$category_nicename is deprecated in /home/calculadsa/www/wp-includes/category.php on line 382

Deprecated: Creation of dynamic property WP_Term::$category_parent is deprecated in /home/calculadsa/www/wp-includes/category.php on line 383

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$object_id is deprecated in /home/calculadsa/www/wp-includes/class-wp-term.php on line 198

Deprecated: Creation of dynamic property WP_Term::$cat_ID is deprecated in /home/calculadsa/www/wp-includes/category.php on line 378

Deprecated: Creation of dynamic property WP_Term::$category_count is deprecated in /home/calculadsa/www/wp-includes/category.php on line 379

Deprecated: Creation of dynamic property WP_Term::$category_description is deprecated in /home/calculadsa/www/wp-includes/category.php on line 380

Deprecated: Creation of dynamic property WP_Term::$cat_name is deprecated in /home/calculadsa/www/wp-includes/category.php on line 381

Deprecated: Creation of dynamic property WP_Term::$category_nicename is deprecated in /home/calculadsa/www/wp-includes/category.php on line 382

Deprecated: Creation of dynamic property WP_Term::$category_parent is deprecated in /home/calculadsa/www/wp-includes/category.php on line 383

Calculadora Conversor > Calculadoras matemáticas > Calculadora de valor absoluto

Otras calculadoras y conversores que te pueden interesar:


Deprecated: Creation of dynamic property WP_Query::$comments_by_type is deprecated in /home/calculadsa/www/wp-includes/comment-template.php on line 1528

3 comentarios en «Calculadora de valor absoluto»

  2. Mi cuestión es la siguiente, tengo que demostrar que en el conjunto Z se cumplen las propiedades siguientes:

    |a+b| es menor o igual a |a+b|
    |a-b| es menor o igual a |a-b|
    |a| × |b| es igual a |a×b|
    |a| / |b| es igual a |a/b|

    No logro comprender.

    Responder

Deja un comentario

Información sobre protección de datos

  • Responsable: Ignacio Cuesta
  • Fin del tratamiento: Controlar el spam, gestión de comentarios
  • Legitimación: Tu consentimiento
  • Comunicación de los datos: No se comunicarán los datos a terceros salvo por obligación legal.
  • Derechos: Acceso, rectificación, portabilidad, olvido.
  • Contacto: contacto@calculadoraconversor.com.
  • Información adicional: Más información en nuestra política de privacidad.


Deprecated: Creation of dynamic property WP_Term::$cat_ID is deprecated in /home/calculadsa/www/wp-includes/category.php on line 378

Deprecated: Creation of dynamic property WP_Term::$category_count is deprecated in /home/calculadsa/www/wp-includes/category.php on line 379

Deprecated: Creation of dynamic property WP_Term::$category_description is deprecated in /home/calculadsa/www/wp-includes/category.php on line 380

Deprecated: Creation of dynamic property WP_Term::$cat_name is deprecated in /home/calculadsa/www/wp-includes/category.php on line 381

Deprecated: Creation of dynamic property WP_Term::$category_nicename is deprecated in /home/calculadsa/www/wp-includes/category.php on line 382

Deprecated: Creation of dynamic property WP_Term::$category_parent is deprecated in /home/calculadsa/www/wp-includes/category.php on line 383

Deprecated: Use of "parent" in callables is deprecated in /home/calculadsa/www/wp-content/plugins/wp-rocket/inc/Dependencies/Minify/JS.php on line 127