Calcular área del cono

¿Necesitas calcular el área de un cono? Usa nuestra calculadora y podrás hacerlo de forma inmediata a partir del radio de la base y la longitud de la generatriz de esta figura geométrica.

Para obtener el área del cono sólo tienes que rellenar estos datos en la calculadora y pulsar el botón de calcular, eso sí, recuerda que tanto el radio como la generatriz deben ir en las mismas unidades para que el resultado obtenido sea el correcto. Si por ejemplo tienes el radio en centímetros y la generatriz en metros, deberás convertir una de ellas para que coincidan.

Fórmula para calcular el área de un cono

Para calcular el área de un cono hay dos fórmulas que podemos aplicar en función de si queremos calcular el área lateral o el área total de la figura:

• El área lateral es la suma de todas las caras laterales del cono y se representa con las siglas A_L.
• El área total es la suma de las caras laterales y el de la base de la figura. En este caso se representa con A_T.

La fórmula a usar en cada caso es la siguiente:

Área lateral = π x radio x generatriz

Área total = π x radio x (generatriz + radio)

Como hemos dicho al principio, es imprescindible que las medidas de la generatriz y el radio estén en las mismas unidades (todo en centímetros, todo en metros, etc. pero nunca una puede ir en centímetros y la otra en metros).

¿Cómo calcular el área de un cono a partir de su altura?

Si los datos del problema nos da la altura del cono pero no la longitud de su generatriz, no pasa nada. Podemos calcular el área de la figura igualmente aunque vamos a tener que aplicar alguna fórmula más en el proceso.

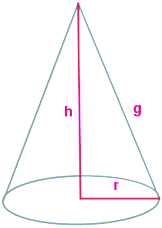
Si os fijáis en la representación del cono que tenéis encima de estas líneas podéis ver que la altura, el radio y la generatriz forman un triángulo rectángulo, lo que nos permite aplicar el Teorema de Pitágoras. Por lo tanto tenemos que:

g² = r² + h²

Despejamos la incógnita que nos dará el valor de la generatriz del cono y tenemos que:

g = √(h² +r²)

Vamos a verlo con un ejemplo práctico. Tenemos que calcular el área de un cono de 6 centímetros de altura y 4 centímetros de diámetro. Lo primero de todo va a ser calcular la longitud de la generatriz a partir de la fórmula anterior:

g = √(h² + r²) = √(36 + 4) = 6,32 centímetros

Fíjate en que nos han dado el valor del diámetro de la base por lo que hemos tenido que dividir entre dos para sacar el radio.

Ahora ya podemos calcular el área del cono a partir de la fórmula:

Área lateral = π x radio x generatriz = π x 2 x 6,32 = 39,69 cm²

Área total = π x radio x (generatriz + radio) = π x 2 x (2 + 6,32) = 52,25 cm²

¿Es fácil, no? Si tienes alguna duda para hallar el área de un cono déjanos un mensaje y te ayudaremos lo antes posible.

Si lo que quieres es calcular el volumen de un cono puedes hacer click en el enlace que te acabamos de dejar y podrás hacerlo.

Nacho

Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.