Calcular el volumen de un cono es algo bastante fácil siempre y cuando nos acordemos de la fórmula que hay que aplicar, desgraciadamente, esto no siempre sucede así que para estos casos hemos creado una calculadora online que te hallará el volumen del cono a partir de su altura y el radio de la base. Introduce ambos datos en la herramienta que tienes a continuación, pulsa el botón de calcular y obtendrás el volumen de la figura.
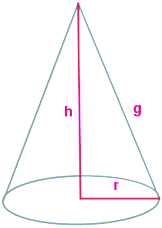
En el caso de que nos den la longitud de la generatriz (g), podemos calcular la altura (h) o el radio (r) a partir del Teorema de Pitágoras (es un triángulo rectángulo como puedes comprobar en la fotografía). Luego escribimos los resultados en la calculadora y listo. Si lo que quieres es calcular el área del cono, pulsa el enlace que te acabamos de dejar y podrás hacerlo.
Contenido de este artículo
Cómo calcular el volumen de un cono
Para calcular manualmente el volumen de un cono tenemos que elevar al cuadrado el valor del radio, multiplicar el resultado por la altura y por el número PI. Cuando tengamos hechas esas tres multiplicaciones, es necesario dividir la cantidad entre tres para obtener el volumen final. Esto se resume en la siguiente fórmula matemática:
Como ves, se trata de una fórmula muy sencilla pero difícil de recordar y es que si no calculamos volúmenes con regularidad, este tipo de cosas las vamos olvidando. Por suerte, queremos que no dependas de las fórmulas y por eso, te ofrecemos una calculadora que hace todas las operaciones por ti.
Ejercicios para calcular el volumen de un cono
Como ejemplo práctico de la teoría vista en el punto anterior, vamos a imaginar que tenemos un cono con altura de 12 centímetros y cuya base tiene un diámetro de 6 centímetros.
Aplicamos la fórmula para obtener el volumen de un cono y tenemos que:
V = (π x 32 x 12) / 3 = 113,094 cm3
Fíjate que en el enunciado del ejercicio para calcular el volumen del cono nos dan el diámetro de la base y no el radio que es el valor que necesitamos. Por eso dividimos el diámetro entre dos y lo elevamos al cuadrado.
Ejemplo con generatriz del cono
Vamos a ver otro ejemplo en el que nos piden calcular el volumen de un cono a partir de su generatriz que mide 8 cm y el radio de la base que mide 3 centímetros.
En este caso lo primero que tenemos que hacer es hallar el valor de la altura del cono (h) a partir de su generatriz (g) y el radio (r) de la base. Para ello, hacemos uso del teorema de Pitágoras que nos dice que:
g2 = r2 + h2
Despejamos la incógnita que nos dará el valor de la altura y tenemos que:
h = √(g2 - r2) = √(64 - 9) = 7,416 centímetros.
Ahora que ya tenemos la altura del cono, podemos aplicar la fórmula para calcular su volumen:
V = (π x 9 x 7,416) / 3 = 69,892 cm3
Si tienes alguna duda de cómo calcular el volumen de esta figura, déjanos un comentario y te ayudaremos lo antes posible.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.