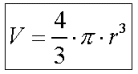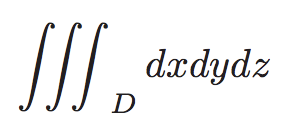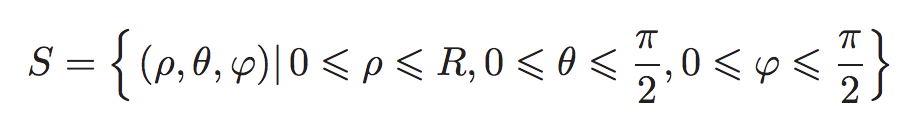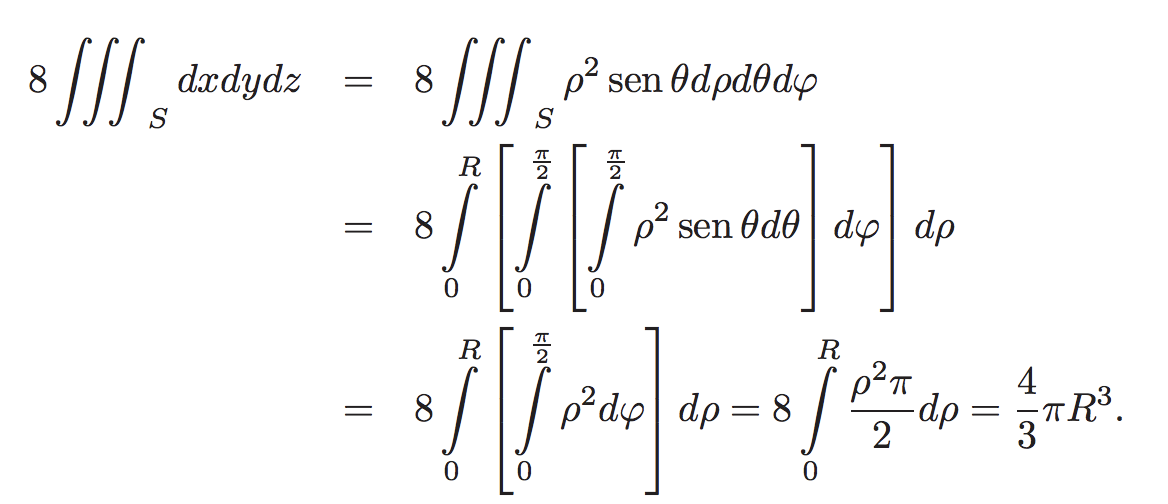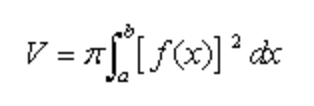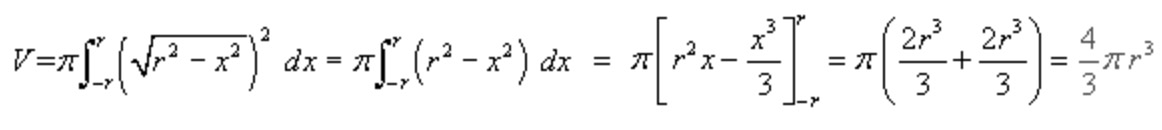Si ya has calculado el área de una esfera y ahora te interesa conocer su volumen, a continuación tienes la calculadora para conocer el volumen de una esfera.
Sólo tienes que introducir el radio de la esfera y presionar el botón de calcular para obtener el volumen de esta figura. Nuestra herramienta te proporcionará el resultado en dos formas posibles de representación para que escojas la que más útil te sea:
Contenido de este artículo
¿Cómo se calcula el volumen de la esfera de radio r?
Para hallar el volumen de una esfera, simplemente tienes que elevar al cubo el radio. El resultado que obtengas lo tienes que multiplicar por PI y, por último, multiplicarlo por 4/3.
Fórmula para calcular el volumen de una esfera
La teoría que acabamos de ver se puede resumir en la siguiente fórmula matemática que te servirá para calcular el volumen de una esfera de radio r:
Por ejemplo, vamos a calcular el volumen de una espera que tiene como radio = 2 centímetros:
V = 4/3 x π x 23 = 10,66π centímetros cúbicos = 33, 51 cm3
Ten en cuenta que en la fórmula utilizamos el radio de la esfera y no su diámetro. Si en el enunciado del problema nos dan el diámetro, lo único que tenemos que hacer es dividir su valor entre 2:
radio de una esfera = diámetro / 2
Una vez que sepamos cuánto vale el radio de la esfera, aplicamos la fórmula que tenemos más arriba.
Demostración del volumen de una esfera
Existen varias formas de demostrar la fórmula del volumen de una esfera. Vamos a ver las más comunes:
Con integrales triples o de volumen
Se puede demostrar la fórmula para calcular el volumen de una esfera mediante el uso de integrales triples o volumétricas.
Para demostrar la fórmula del volumen de una esfera con centro en el origen y radio R sabemos que los puntos que hay en el primer octante se pueden expresar como:
Por lo tanto, podemos resolver la integral triple para hallar la fórmula del volumen de una esfera tal y como se puede ver aquí:
Otra forma de hacerlo con integrales triples:
Con integrales simples
Si las integrales triples son demasiado complejas para ti, existe otra forma de obtener la demostración del volumen de una esfera usando integrales definidas.
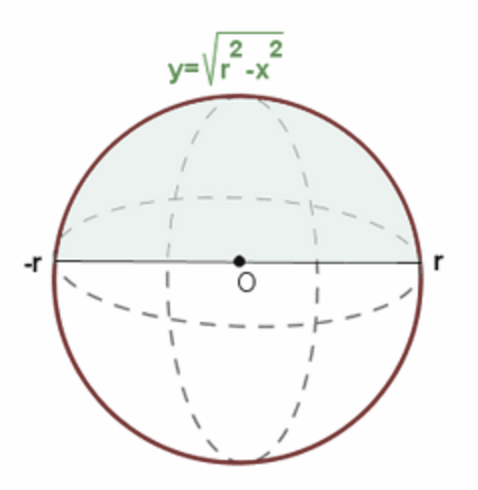
Para ello vamos a partir de la ecuación de la circunferencia que es esta:
x² + y² = r²
Si giramos un semicírculo alrededor del eje de abscisas tendremos como resultado una esfera.
Existe una integral que nos permite calcular el volumen del cuerpo de revolución que se genera al hacer girar una curva f(x) al rededor del eje OX y limitado por x = a y x = b aunque en nuestro caso viene limitado por -r y r. Esta integral es la siguiente:
Qué adaptándola a nuestro caso particular de la esfera se transforma en esto:
Calcular la superficie de una esfera
Si en lugar de calcular el volumen quieres calcular la superficie de una esfera, también tenemos una calculadora para esta finalidad.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.