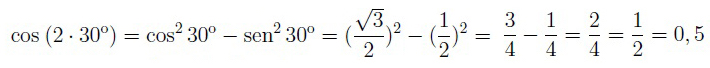Calcula el coseno de cualquier ángulo en grados o radianes con nuestra calculadora matemática online que te permitirá averiguar con facilidad el valor de esta razón trigonométrica.
El funcionamiento de esta calculadora de cosenos online es muy fácil. Simplemente tienes que introducir el valor del ángulo y seleccionar el tipo de unidades (grados o radianes). A continuación pulsa el botón de calcular y listo, automáticamente conocerás el coseno del ángulo que has introducido. Recuerda que el coseno de un ángulo sólo puede tomar valores comprendidos entre -1 y 1.
Recuerda que también tenemos a tu disposición otras calculadoras relacionadas con el mundo de la trigonometría:
Contenido de este artículo
Cómo calcular el coseno
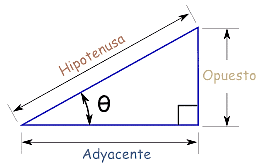
Si nos dan un triángulo rectángulo como el de la imagen y nos piden calcular el coseno, tendremos que dividir el cateto adyacente entre la hipotenusa.
Esa sería la fórmula básica para calcular esta razón trigonométrica.
Gráfica del coseno
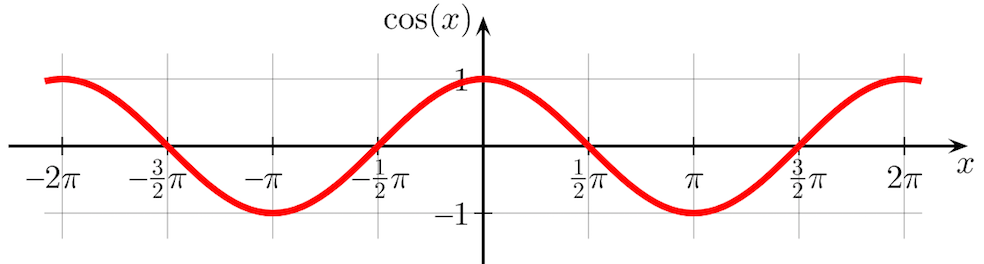
Aquí tenéis una representación gráfica de la función cos(x) en la que se puede ver todos los valores que adopta en el intervalo [-2π, 2π].
Como puede observarse, se trata de una función periódica cuyo dominio pertenece a todos los números reales. A continuación encontrarás una tabla con los principales valores que adopta esta función trigonométrica en todo su intervalo.
Por ejemplo, en la gráfica se puede ver perfectamente que el coseno de pi es igual a -1.
Tabla de la función coseno
Si necesitas conocer de un vistazo los valores del coseno de los principales ángulos, a continuación tienes una recopilación que te será muy útil en los problemas de trigonometría.
| Grados | Radianes | Coseno |
|---|---|---|
| 0º | 0 | 1 |
| 30º | π/6 | 0,866 |
| 45º | π/4 | 0,707 |
| 60º | π/3 | 0,5 |
| 90º | π/2 | 0 |
| 180º | π | -1 |
| 270º | 3π/2 | 0 |
| 360º | 2π | 1 |
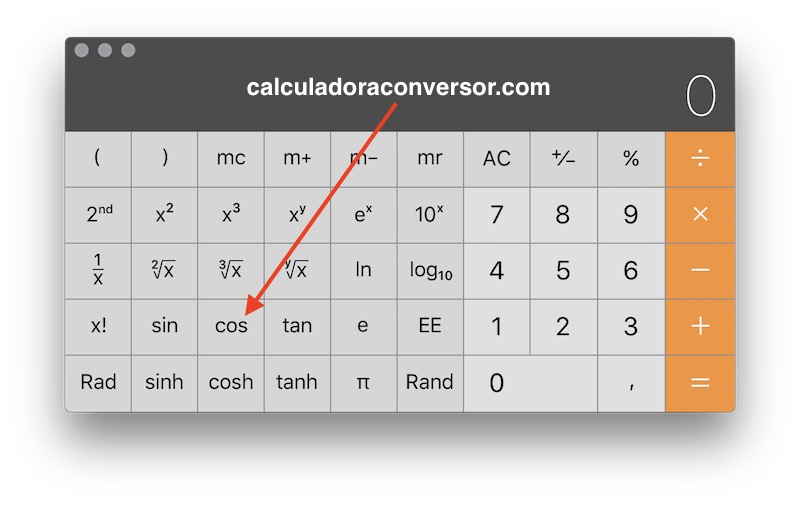
Cómo sacar el coseno de un ángulo con calculadora
Si quieres sacar el coseno de un ángulo con la calculadora científica, lo primero que debes verificar es si está configurada en grados o en radianes. Esto es vital ya que no es lo mismo 60 grados que 60 radianes. Si quieres más información, en nuestro conversor de grados a radianes te explicamos con más detenimiento las diferencias entre estados dos formas de expresar ángulos.
Una vez que tengas claro el punto anterior, calcular el coseno con la calculadora es muy fácil. Simplemente pulsa la tecla que pone COS, escribe el ángulo y pulsa la tecla = para obtener el resultado.
Por ejemplo, si quieres calcular el coseno de 45 deberás pulsar la siguiente combinación de teclas:
COS → 45 → =
Y automáticamente saldrá en la pantalla que el coseno de 45 es igual a 0,707.
Calcular coseno en Excel
Hay otra forma de calcular el cos de un ángulo usando Excel y una función que lleva precisamente ese nombre. Eso sí, por defecto Excel trabaja en radianes así que atento a la fórmula que debes usar en cada caso.
Si quieres calcular el COS en radianes, debes escribir la siguiente fórmula en Excel:
=COS()
Y entre los paréntesis escribes el ángulo expresado en rads.
Si quieres calcular el coseno de un ángulo en grados, deberás escribir la fórmula de esta forma:
=COS(RADIANES(90))
En este caso hemos obtenido el coseno de 90 pero puedes cambiar el número por el ángulo en grados que tú quieras.
Derivada del coseno
La derivada del coseno de x es igual al menos seno de x. Matemáticamente esto se puede expresar mediante la siguiente forma:
f(x) = cosx → f'(x) = - senx
Si en lugar de x tenemos una función u, entonces la derivada será igual a la derivada de la función u multiplicada por el menos seno de u. Esto quedaría expresado matemáticamente así:
f(x) = cosu → f'(x) = - u' senu
Estas son las derivadas básicas de la función COS.
Integral del coseno
Ya sabes que la integral es la operación contraria a derivar por lo que podríamos deducirla a partir de la teoría vista en el punto anterior. De todas formas vamos a ponértelo fácil y aquí tienes cuál es la integral del coseno de x:
∫cosx dx = senx + C
Si tenemos la integral del coseno de una función u por su derivada, entonces el resultado de la integral será:
∫cosu · u' dx = senu + C
Si te ha quedado alguna duda o tienes una pregunta sobre el cos, nos puedes escribir un comentario y te echaremos una mano lo antes posible. Y si te ha gustado, pues comparte en las redes sociales o déjanos otro comentario agradeciéndonos nuestra labor, que eso también nos gusta :D
Teorema del coseno
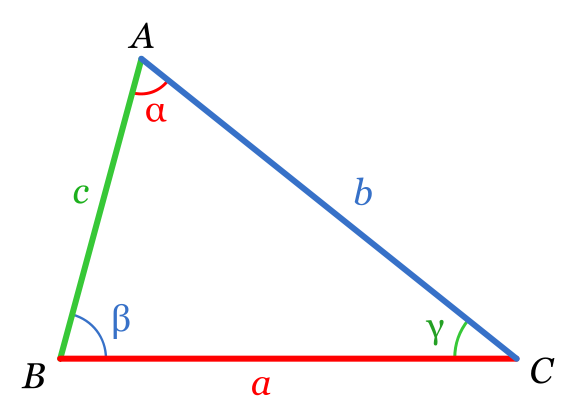
El Teorema del coseno (también conocido como ley de cosenos), nos permite calcular los lados los ángulos que nos falten, relacionando uno de los lados del triángulo con los dos restantes y el coseno del ángulo que forman.
Por si no ha quedado muy clara la explicación teórica, a continuación tienes todas las fórmulas del Teorema del coseno que te servirán de ayuda para resolver triángulos:
a2 = b2 + c2 - 2bc·cosA
b2 = a2 + c2 - 2ac·cosB
c2 = a2 + b2 - 2ab·cosC
Si te fijas en cada una de las fórmulas, todas responden al mismo patrón de cálculo:
- Elevar al cuadrado los dos lados que conocemos y sumar su valor
- Calcular el coseno del ángulo opuesto al lado que queremos calcular y mutliplicarlo por el doble de los dos lados que conocemos
- Restar el resultado obtenido en el punto 1 menos el del punto 2.
Combinando el Teorema del coseno con el Teorema del seno, podemos resolver triángulos de forma sencilla y eficaz.
Coseno del ángulo suma
La fórmula del coseno del ángulo suma es la siguiente:
cos (a + b) = cosa · cosb + cosa·senb
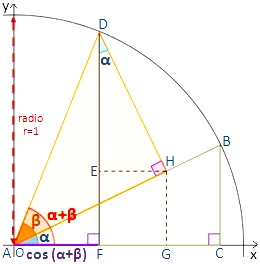
La demostración del coseno del ángulo suma se deduce calculando cuánto vale el segmento AF:
AF = AG - FG = AG - EH = cos(α+β)
También sabemos que:
EH = DH senα
DH = senβ
Sustituimos y queda que:
EH = senβ senα
Ahora calculamos cuánto valen los segmentos AG y EH,
AG = AH cosα
AH = cosβ
Sustituimos y tenemos que:
AG = cosβ cosα
Finalmente, sustituimos en la primera ecuación que tenemos al principio de la demostración y nos queda que:
cos(α+β) = cosα cosβ - senα senβ
Coseno del ángulo doble
A continuación tienes la fórmula del coseno del ángulo doble:
cos2a = cos2a - sen2a
El ángulo doble (2a) tiene sus propias razones trigonométricas y el cos del ángulo doble es una de ellas, una fórmula que se deduce a partir de la fórmula del coseno del ángulo suma que hemos visto en el punto anterior (α = β)
Por ejemplo, vamos a resolver este ejercicio en el que obtendremos el cos del ángulo doble de 30º:
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.