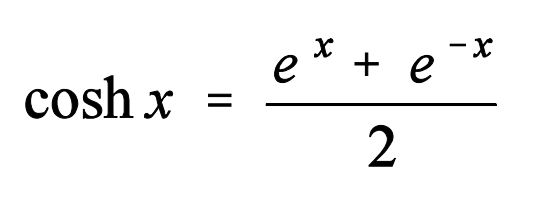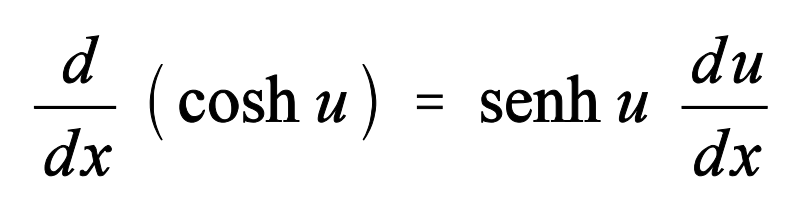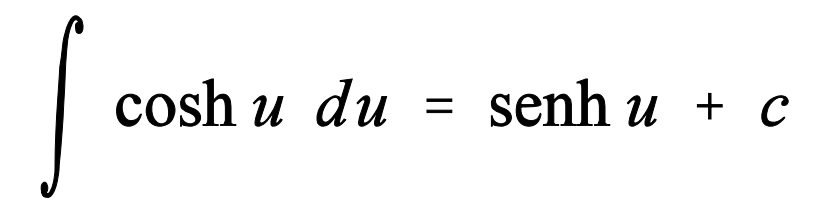¿Necesitas calcular el coseno hiperbólico de un número real x? Usa nuestra calculadora y obtendrás automáticamente el resultado de esta función hiperbólica de la que conoceremos más datos en los siguientes puntos.
Para usar la calculadora del coseno hiperbólico sólo tienes que escribir el número x para el cual quieres sacar su cosh y pulsar el botón de calcular para obtener el resultado.
Contenido de este artículo
Propiedades del coseno hiperbólico
El coseno hiperbólico tiene una serie de propiedades que debes conocer para resolver los ejercicios de las funciones hiperbólicas con mayor facilidad.
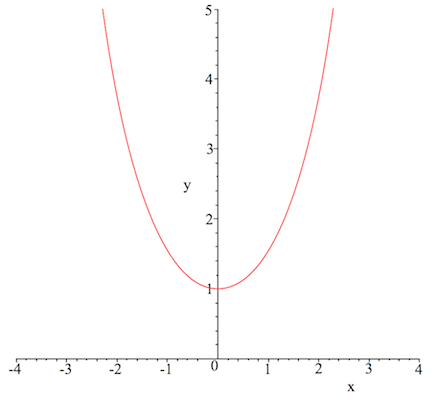
Su dominio va desde (-∞, +∞) y se trata de una función biyectiva en el codominio [1, +∞), par, convexa y trascendente. Todas estas propiedades pueden verse reflejadas en la representación gráfica de la función cosh (x) que tenéis unas líneas más arriba.
Además, hay una serie de relaciones que también son muy importantes:
- cosh (x + y) = coshx coshy + senhx seny
- cosh (x - y) = coshx coshy - senhx seny
- cosh 2x = cosh2x + senh2x
- cosh2(x) = 1 + sinh2 (x)
Coseno hiperbólico de 0
¿Cuánto es el coseno hiperbólico de 0? Para resolver esta duda vamos a fijarnos en la fórmula de la función cosh(x) y que es la que tenemos justo encima de estas líneas.
En este caso tenemos que x = o, por lo tanto, sustituimos y tenemos que:
cosh(0) = (e0 + e-0) / 2 = 1
Esto es así porque cualquier exponencial elevada a la cero nos dará 1 como resultado, por lo tanto, el coseno hiperbólico de 0 es igual a 1.
Si te fijas, el resultado que hemos obtenido cuadra perfectamente con lo que vemos en la gráfica de la función cosh (x)
Derivada del coseno hiperbólico
La derivada de una función con cosh es igual a la fórmula que tenéis justo encima de estas líneas. Si en lugar de una función se traba de un número real x, la derivada será la siguiente:
d/dx cosh(x) = sinh(x)
Por lo tanto, la derivada del coseno hiperbólico de x es igual al seno hiperbólico de x.
Integral del coseno hiperbólico
Llegados a este punto, también es interesante que conozcas la integral del coseno hiperbólico que tras realizar la demostración, nos dará que es igual al senh (u) + c.
Calcular Cosh (x) en Excel
Además de usar nuestra calculadora del coseno hiperbólico, también puedes calcular el cosh de cualquier número real usando Excel y la siguiente función:
=cosh()
Entre paréntesis tienes que escribir el número para el cual quieres calcular su cosh o apuntar hacia una celda en la que hayas escrito dicha cifra.
Sin duda, es otro método alternativo para comprobar que el resultado del ejercicio que hemos hecho es correcto.
¿Te ha quedado alguna duda sobre la función hiperbólica cosh? Si es así, déjanos un comentario y trataremos de ayudarte lo antes posible.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.