¿Necesitas calcular los divisores de un número online? Utiliza nuestra calculadora y obtendrás todos números enteros y factores primos entre los que se puede dividir ese número entero.
Su funcionamiento es muy sencillo. Sólo tienes que escribir el número entero (sin comas ni decimales) para el cuál quieres obtener los divisores y, a continuación, presionar sobre el botón de Calcular para obtener el resultado.
Contenido de este artículo
¿Qué son los divisores de un número?
Se denomina divisores de un número a aquellos valores que nos permiten hacer una división exacta a esa cantidad, es decir, el resto que obtenemos es cero. Por ejemplo, si 2 es divisor de 100, podemos decir que:
- 2 es divisor de 100
- 100 es divisible entre 2
- 2 es múltiplo de 100
Cualquiera de las tres afirmaciones anteriores sería correcta y vienen a expresar lo mismo aunque contado con otras palabras. Expresado matemáticamente, esto se resume a que
a es divisor de b si b/a = 0
Cómo calcular cuántos divisores tiene un número rápidamente
Existe un método muy rápido para averiguar cuántos divisores tiene un número de forma muy rápida. Estos son los pasos a seguir:
- Descomponer el número en factores primos
- Multiplicar los exponentes de la descomposición en factores primos pero aumentados en una unidad.
Por ejemplo, si descomponemos en factores primos el número 432, nos queda que es igual a
432 = 24 x 33
¿Cuántos divisores tendrá? Para eso multiplicamos los exponentes de los factores primos pero aumentados en una unidad. Es decir:
(4+1) x (3 + 1) = 5 x 4 = 20
Por lo tanto, 432 tendrá un total de 20 divisores. Puedes usar nuestra calculadora de divisores para comprobar que la respuesta que hemos obtenido es correcta.
Cómo calcular los divisores de un número
Para calcular los divisores de un número tenemos que tener en cuenta los criterios de divisibilidad. Además, el 1 y el propio número siempre serán divisores pero el resto tendremos que calcularlos.
Si el número es pequeño, podemos ir haciendo divisiones manualmente o con la calculadora para ver si la división es exacta y ese número es divisor. Sin embargo, si no recuerdas esos criterios de divisibilidad o el número es muy grande, existe un método mecánico para hacerlo que veremos con el número 432 que vimos en el apartado anterior.
Lo primero de todo será hacer su descomposición factorial, que ya tenemos resuelta:
432 = 24 x 33
A continuación creamos una tabla en la que colocaremos las potencias de 2 desde 20 hasta 24 en la fila superior. En la columna izquierda pondremos las potencias de 3 que van desde 30 hasta 33. Por si te es de utilidad, encima de estas líneas encontrarás un vídeo en el que explican el método que vamos a usar para resolver los ejemplos pero con otras cantidades para que sigas practicando de cara a un examen.
| 20↓ | 21↓ | 22↓ | 23↓ | 24↓ | |
|---|---|---|---|---|---|
| 30→ | 1 | 2 | 4 | 8 | 16 |
| 31→ | 3 | ||||
| 32→ | 9 | ||||
| 33→ | 27 |
Con los valores ya colocados en la tabla, el siguiente paso para obtener los divisores de un número consiste en multiplicar a cada número de la primera columna por cada número de la primera fila. Es decir, para completar la segunda fila tendremos que resolver las siguientes multiplicaciones:
- 3 x 2
- 3 x 4
- 3 x 8
- 3 x 16
A continuación rellenaremos la siguiente fila resolviendo las siguientes multiplicaciones:
- 9 x 2
- 9 x 4
- 9 x 8
- 9 x 16
Y así sucesivamente hasta completar la tabla entera.
Si lo hemos hecho bien, nos quedará con el siguiente aspecto:
| 20↓ | 21↓ | 22↓ | 23 ↓ | 24↓ | |
|---|---|---|---|---|---|
| 30→ | 1 | 2 | 4 | 8 | 16 |
| 31→ | 3 | 6 | 12 | 24 | 48 |
| 32→ | 9 | 18 | 36 | 72 | 144 |
| 33→ | 27 | 54 | 108 | 216 | 432 |
Ya tenemos los 20 divisores del número 432 calculados. Este proceso lo puedes repetir para cualquier otro número. Lo único que debes de tener en cuenta es que si el número tiene más de dos factores primos, tendrás que dividir el proceso en varios pasos.
Ejemplo resuelto
Vamos a calcular los divisores del número 360. Como hemos visto en el punto anterior, lo primero que tenemos que hacer es proceder a su descomposición en factores primos:
360 = 23 x 32 x 5
A continuación generamos la tabla con las potencias de 2 y 3 tal y como hemos explicado anteriormente:
| 20↓ | 21↓ | 22↓ | 23 ↓ |
|
|---|---|---|---|---|
| 30→ | 1 | 2 | 4 | 8 |
| 31→ | 3 | 6 | 12 | 24 |
| 32→ | 9 | 18 | 36 | 72 |
Nos falta tener en cuenta el factor primo 5, para lo cual construiremos una nueva tabla que tendrá en la primera fila los números obtenidos en la tabla anterior. En la columna izquierda colocaremos las potencias de 5:
| 50→ | 1 | 2 | 3 | 4 | 6 | 8 | 9 | 12 | 18 | 24 | 36 | 72 |
| 51→ | 5 | 10 | 15 | 20 | 30 | 40 | 45 | 60 | 90 | 120 | 180 | 360 |
Ahora sí, ya tenemos todos los divisores de 360 calculados.
Si después de nuestra explicación te ha quedado alguna duda o no sabes cómo encontrar los divisores para un número en concreto, escríbenos un comentario y te ayudaremos a despejar tus inquietudes lo antes posibles.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.
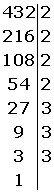

Súper, me ayudó mucho con mis divisores grandes, ¡muchas gracias!
Genial Deisy, gracias!