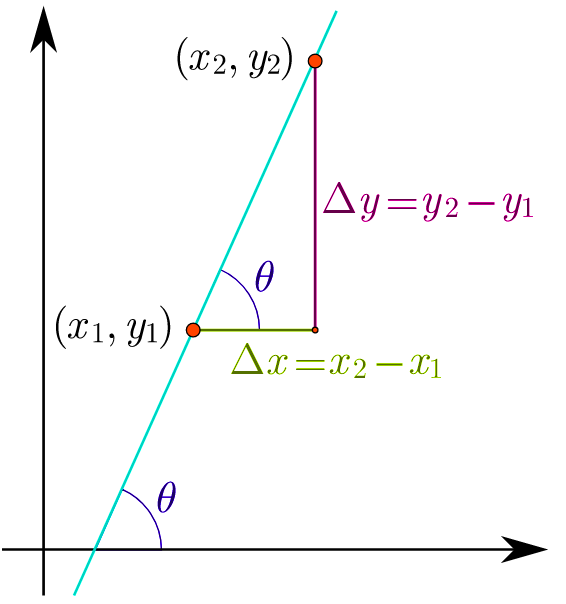
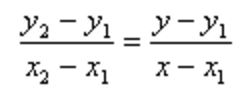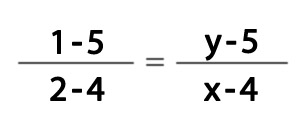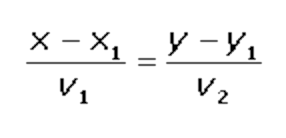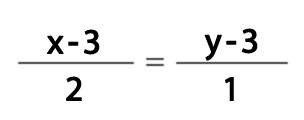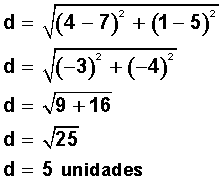Usa nuestra calculadora y te daremos la ecuación de la recta que pasa por dos puntos así como el valor de su pendiente.
Sólo tienes que introducir las coordenadas (x1, y1) (x2, y2) de cada uno de los puntos conocidos y pulsar el botón de calcular para obtener el resultado. Si quieres saber cómo encontrar la ecuación de la recta y ver ejercicios resueltos de cada caso, sigue leyendo más abajo.
Contenido de este artículo
Ecuación punto-pendiente de la recta
La ecuación punto-pendiente es una de las más utilizadas en problemas de matemáticas y es del tipo:
y - y1 = m (x - x1)
Con ella, podemos calcular la ecuación de la recta conociendo la pendiente (m) y un punto P de coordenadas (x1, y1).
Por ejemplo, vamos a calcular la ecuación de la recta si sabemos que tiene una pendiente m=3 y pasa por el punto P = (4,3). Simplemente sustituimos en la ecuación general de la recta y obtenemos:
y - 3 = 3 (x - 4)
Ahora simplificamos:
y = 3x -12 + 3
y = 3x - 9
Ya tenemos calculada la ecuación de la recta que cumple las condiciones del problema.
Ecuación de la recta que pasa por dos puntos
Si nos dan dos puntos y nos piden calcular la recta que pasa por esas coordenadas, tenemos que usar esta fórmula:
En este caso resolver el problema es bastante sencillo ya que sólo tenemos que sustituir en la ecuación y simplificarla lo máximo posible. Para ver cómo se hace, haremos un ejercicio en el que nos piden calcular la ecuación de la recta que pasa por los puntos (4, 5) y (2, 1):
Ahora simplemente tenemos que igualar y simplificar y nos queda la ecuación de esta forma:
2 (x - 4) = y - 5
Simplificamos:
2x - 8 = y - 5
2x - y + 3 = 0
Ya tenemos la ecuación general de la recta que pasa por los dos puntos del enunciado del ejercicio. De aquí también podríamos calcular la pendiente como hemos visto en el apartado anterior:
m = - A / B = - (2 / -1) = 2
Ecuación continua de la recta
Usaremos la ecuación continua de la recta cuando nos den un punto P de coordenadas (x1, y1) y su vector director de coordenadas (v1, v2).
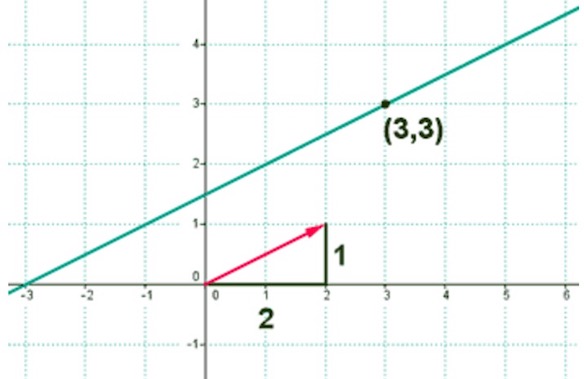
Por ejemplo, en el caso de la gráfica que tenemos encima de estas líneas y en la cual tenemos el punto (3, 3) con vector director (2, 1), la ecuación de la recta sería:
Simplificando nos queda:
x - 3 = 2 (y - 3)
x - 3 = 2y - 6
x - 2y +3 = 0
Ecuación general de la recta
La ecuación general de la recta es del tipo:
Ax + By + C = 0
Siendo A, B y C números Reales y B ≠ 0.
De esta ecuación también podemos sacar:
- La pendiente de la recta (m = - A/B).
- La ordenada en el origen (- C/B).
Con esos datos ya tenemos información suficiente para representar la recta sobre el plano XY.
Ecuaciones paramétricas de la recta
Estas ecuaciones se consiguen a partir de la ecuación vectorial y son de este tipo:
x = x0 + v1t
y = y0 + v2t
Siendo:
- (x0, y0) las coordenadas de un punto de la recta
- (v1, v2) son las coordenadas de un vector en la dirección de la recta
Cómo saber si un punto pertenece a una recta
Para saber si un punto pertenece a una recta dada simplemente tenemos que coger la ecuación de esa recta y sustituir en 'x' e 'y' los valores del punto que nos dan. Si la igualdad se cumple, el punto pertenecerá a la recta y si no se cumplen, entonces no.
Por ejemplo, ¿se encuentra en la recta el punto (1, 3) con ecuación y = 2 +3x? Vamos a verlo:
3 ≠ 2 + 3 → no se cumple la igualdad así que el punto (1,3) no está en la recta.
¿Y el punto (1, 5)?
5 = 2 + 3 → se cumple la igualdad, por lo tanto, el punto (1, 5) está en la recta.
Fórmula para calcular la distancia entre dos puntos de la recta
La distancia entre dos puntos de una recta en el plano cartesiano se puede calcular de forma muy sencilla. Para entenderlo mejor, vamos a verlo con un ejemplo.
Imagina que tienes dos puntos en el plano cuyas coordenadas son:
- P1 (X1, Y1)
- P2 (X2, Y2)
La distancia que separa ambos puntos se obtiene aplicando la siguiente fórmula matemática:
Por ejemplo, vamos a calcular la distancia entre dos puntos con un ejemplo práctico en el que:
- P1 (7, 5)
- P2 (4, 1)
Aplicando la fórmula anterior, tenemos que la distancia existente entre estos dos puntos del plano cartesiano es:
Como ves, saber la distancia entre dos puntos es muy fácil.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.