Si necesitas conocer la descomposición en factores de un número, estás en el lugar adecuado. Aquí encontrarás una calculadora que te permitirá conocer al instante la factorización de cualquier número entero positivo.
En el caso de que introduzcas un número que no se puede descomponer en factores, también te mostrará que la cifra que has escrito se trata de un número primo.
Contenido de este artículo
¿Qué es la factorización de un número?
Cuando hablamos de factorizar un número, lo que estamos haciendo es descomponerlo como un producto de factores primos que al multiplicarse entre sí, nos da como resultado el número de partida.
Por ejemplo:
- El número 6 puede descomponerse como un producto de 2 x 3
- El número 27 puede descomponerse como un producto de 3 x 3 x 3
Para factorizar un número, hay que realizar divisiones entre sus divisores primos hasta que obtengamos un uno en el cociente. Para hacer esto, se suele utilizar el método de la barra vertical, de tal forma que:
- a la izquierda de la barra, escribimos los cocientes de la división
- a la derecha de la barra, escribimos los divisores primos que obtenemos
Una de las aplicaciones claras de la descomposición en factores primos consiste en calcular el mínimo común múltiplo, algo muy importante para hacer otras operaciones como la suma o resta de fracciones.
Factorizar polinomios
Factorizar polinomios también consiste en descomponer en factores a partir de un factor común y, a continuación, sacar las raíces. Vamos a ver algunos casos en particular.
Diferencia de cuadrados
Son polinomios del tipo:
a2 − b2 = (a + b) · (a − b)
En estos casos podemos descomponer en factores y sacar las raíces con relativa facilidad. Por ejemplo, si tenemos:
x2 − 25 = (x2 + 5) · (x2 − 5)
Las raíces del polinomio anterior son x=5 y x=-5
Polinomios de segundo grado
En este caso, la apariencia del polinomio es de este tipo:
ax2 + bx + c = 0, siendo a distinto de cero
También hay variaciones que pueden hacer que simplificar este tipo de polinomios se haga de una forma u otra, por eso, te recomendamos que te pases por la siguiente web en la que te explicamos cómo resolver ecuaciones de segundo grado.
En el enlace que te acabamos de dejar aprenderás a factorizar polinomios de segundo grado.
Cómo factorizar online
Nuestra calculadora para factorizar online tiene un funcionamiento muy sencillo. Sólo tienes que escribir el número que quieres descomponer en factores primos y pulsar el botón de calcular para obtener su factorización.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.
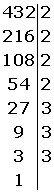

Hola, los felicito por su pagina muy buena, pero quiero decirles que existe un pequeño error y sería genial que lo corrijan para no desinformar a los demás, en el ejercicio x^4-25 sale que las raíces son 5 y -5, pero en realidad es (raiz cuadrada de 5) y menos raiz cuadrada de 5) eso, gracias…
Efectivamente Victor, tienes razón y había una errata en ese enunciado. Ya lo hemos corregido así que muchas gracias por avisar.
Un saludo!
Alguien me ayuda a como resolverlo tio pero esta muy chula la pagina eso si xD
Hola Eduardo,
Dinos que número quieres descomponer en factores y te ayudamos.
Saludos!
quiero descomponer 437896 para acabr mis deberes de mates
Ahí lo tienes: 2 x 2 x 2 x 127 x 431
muchisimas gracias de verdad te voy a donar al final a la mejor caculadora del mundo muchas gracias enseri encima con un ayudznte educado y atebto cada hora opara ber los comentarios dela gente gracias de verdad 5 estrellas
Hola.
Necesito expresar como producto de primos a un número formado por 97 unos (1111…111). ¿Podrían ayudarme?
Gracias
Hola Javier,
No te puedo decir el resultado de la factorización porque el número es muy grande y se produce un desbordamiento, por lo que el resultado que nos arroja es incorrecto: 5 x 811 x 185483 x 6229507 x 2267
He probado a resolverlo con Excel y nos pasa exactamente igual.
Me podrian ayudar a hacer am-bm+an-bn porfavor no se como hacerlo
Hola Saúl,
Para descomponer factorialmente la ecuación que nos propones, puedes hacer lo siguiente:
am-bm+an-bn = a(m+n) – b(m+n) = (m+n)(a-b)
Saludos!
hola se puede factorizar un numero negativo?? ejemplo -5 ,-10 -3 ….. etc..
Hola Alberto José,
Sí, un número negativo también se puede factorizar aunque en este caso tendremos varias combinaciones de factorización posibles.
Por ejemplo, para el número negativo -10 tendremos que su factorización puede ser:
2 x -5
-2 x 5
Como ves, ambas combinaciones dan como resultado el número -10.
Saludos!