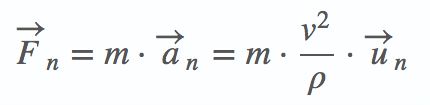¿Quieres calcular la fuerza centrípeta online o aclarar conceptos relacionados con esta fuerza que actúa en objetos en movimiento con trayectorias curvilíneas?
Sigue leyendo y encontrarás una calculadora, la fórmula, ejercicios resueltos y mucho más.
Contenido de este artículo
Calculadora de fuerza centrípeta
Si necesitas calcular la fuerza centrípeta de un objeto, nuestra calculadora puede ayudarte a ello. Sólo tienes que introducir la masa en Kilos del objeto y la aceleración normal que tiene mientras describe su trayectoria curvilínea.
Cuando lo hayas hecho, pulsa el botón de calcular y automáticamente obtendrás el valor de la fuerza centrípeta en Newtons.
Si quieres saber más sobre esta fuerza que experimentan los objetos que describen una trayectoria curva, sigue leyendo y te resolveremos todas las dudas sobre su cálculo.
Concepto de fuerza centrípeta
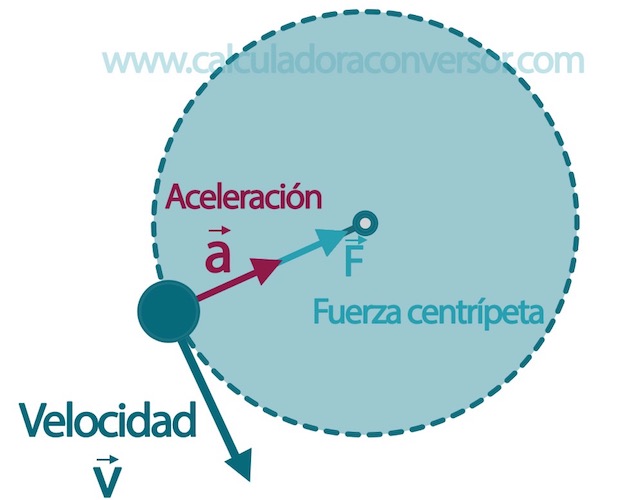
Cuando un objeto realiza una trayectoria curvilínea, el vector de la velocidad tiene que cambiar de dirección y sentido en cada punto por lo que es la aceleración centrípeta la encargada de que esto suceda.
La fuerza centrípeta es la encargada de dotar a ese objeto con dicha aceleración centrípeta.
Como se puede ver en el diagrama que tenéis encima de estas líneas, la fuerza centrípeta es un vector cuya dirección es el radio de la circunferencia y su sentido es hacia el centro. Su módulo es constante.
Diferencia entre fuerza centrípeta y centrífuga
¿Cuál es la diferencia entre fuerza centrípeta y centrífuga? ¿Son lo mismo? Realmente no, a pesar de que ambas estén muy relacionadas entre sí. Veamos cuáles son las diferencias entre ellas.
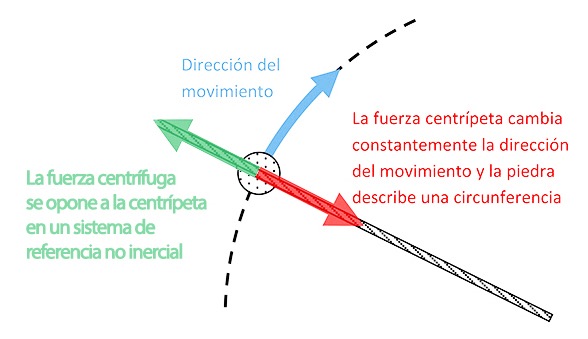
Mientras que la fuerza centrípeta es una fuerza real, la centrífuga es ficticia y nos sirve para explicar la existencia de la fuerza centrípeta en un movimiento circular sobre sistemas de referencia no inerciales.
Si no ha quedado muy clara la explicación, vamos a imaginar que estamos montados en un carrusel de la feria como el de la siguiente fotografía:
Mientras la atracción está en movimiento, cada una de las plataformas describe un movimiento circular y, por lo tanto, tienen aceleración centrípeta como hemos visto en el punto anterior.
Si tienen dicha aceleración centrípeta es porque hay una fuerza que la origina y es la fuerza centrípeta. Esto puede observarse en la tensión de cada una de las cadenas que sujetan las plataformas.
Hasta aquí, no hay nada que no sepamos. Sin embargo, si nosotros nos montamos en una de las plataformas nuestro sistema de referencia se vuelve no inercial ya que nuestra plataforma y nosotros nos movemos a la vez, es decir, tenemos la misma aceleración.
Este sistema de referencia no inercial crea la ilusión de que la plataforma sobre la que estamos montados está en reposo ya que está siempre debajo de nuestros pies, sin embargo, la cuerda de la atracción sigue tensa así que la aceleración centrípeta sigue ahí.
Para darle sentido al reposo de nuestra plataforma, inventamos la fuerza centrífuga como recurso para anular a la fuerza centrípeta. Para que tenga lógica, la fuerza centrífuga tendrá el mismo módulo y dirección pero sentido contrario al de la fuerza centrífuga.
Esta explicación sólo sirve si estamos montado en la atracción (sistema de referencia no inercial)
Fórmula de la fuerza centrípeta
La fórmula de la fuerza centrípeta es la siguiente:
En dicha fórmula podemos distinguir varias variables:
- Fn: es la fuerza centrípeta que queremos calcular. Es importante poner el subíndice 'n' ya que nos ayuda a recordar que su dirección es normal a la trayectoria del movimiento y sirve para diferenciarla de la fuerza centrífuga que veremos a continuación. La fuerza centrípeta se mide en Newton (N)
- m: es la masa del cuerpo y viene dada en kilogramos
- an: es la aceleración normal o aceleración centrípeta. Debe estar en metros por segundo al cuadrado (m/s2). La aceleración normal puede desglosarse en an=v2/ρ, siendo v la velocidad del cuerpo en ese punto de la trayectoria y ρ el radio de curvatura.
Fórmula de la fuerza centrífuga
La fuerza centrífuga no tiene ninguna fórmula ya que se trata de una fuerza ficticia que inventamos tal y como hemos visto un poco más arriba.
Dado que la fuerza centrífuga tiene el mismo valor que la fuerza centrípeta pero con sentido contrario, puedes usar la fórmula de la fuerza centrípeta y ponerle un signo menos (-) al resultado.
Ejemplos de fuerza centrípeta
A continuación te vamos a dar algunos ejemplos de fuerza centrípeta que luego puedes desarrollar como ejercicios resueltos aplicando la fórmula que hemos visto un poco más arriba. Sólo tendrías que dotar de masa al objeto y de aceleración centrípeta.
Coche en una curva
Un coche de 1500 Kg circula por una carretera a 120 kilómetros por hora cuando traza una curvatura cuyo radio es de 100 metros, experimentando así una fuerza centrípeta hasta que sale de dicha curva. ¿Cuál es su valor?
Una bola atada a una cuerda que gira en círculos
Si atamos una bola a un cordel y la hacemos girar en círculos, durante la trayectoria circular la cuerda está soportando la fuerza centrípeta que permite ese giro curvilíneo. Calcula su Fn si la pelota pesa 200 gramos y tiene una aceleración centrípeta de 15m/s2.
¿Se te ocurren más ejemplos de fuerza centrípeta para hacer ejercicios? Si quieres más o tienes algún problema que no sabes resolver, déjanos un comentario y te ayudaremos a solucionarlo.
Fuerza centrípeta igual a fuerza gravitatoria
Existe relación entre la fuerza centrípeta y la fuerza gravitatoria. Newton lo demostró con la Ley de Gravitación Universal en la cual se especifica que toda partícula del universo puede atraer a otra partícula con una fuerza F.
Dicha fuerza varía proporcionalmente en función de las masas de dichas partículas e inversamente proporcional al cuadrado de la distancia que las separa en línea recta.
Esto quiere decir que la fuerza de la gravedad actúa a modo de fuerza centrípeta ya que su vector es radial se dirige hacia el centro de la Tierra.
Un ejemplo claro lo podemos ver con la Tierra y la Luna. La fuerza centrípeta es el campo gravitatorio que ejerce nuestro planeta sobre el satélite (la luna)
Porqué la fuerza centrípeta no realiza ningún trabajo
Hay un motivo por el cual se dice que la fuerza centrípeta no realiza ningún trabajo.
La definición de trabajo nos dice que hay que ejercer una fuerza sobre un objeto y éste tiene que moverse en la dirección de dicha fuerza aplicada.
Sin embargo, la definición de fuerza centrípeta nos dice que ésta tiene una dirección perpendicular a la del movimiento y por eso no realiza ningún trabajo.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.