La calculadora de la Ley de Snell te permite hallar cualquiera de las cuatro incógnitas que intervienen en la fórmula para calcular el ángulo de refracción de la luz al pasar de un medio a otro con distinto índice de refracción.
Sólo tienes que seleccionar alguna de las siguientes variables en la calculadora de la Ley de Snell:
- n1: índice de refracción del primer medio
- n2: índice de refracción del segundo medio
- Ángulo de incidencia (escrito en grados)
- Ángulo del rayo refractado (también en grados)
Cuando tengas seleccionada la variable, rellena los valores del resto de incógnitas y pulsa el botón de calcular para conocer el resultado. Si tienes los ángulos de incidencia o refracción en radianes, aquí puedes pasarlos a grados.
Contenido de este artículo
Fórmula de la Ley de Snell
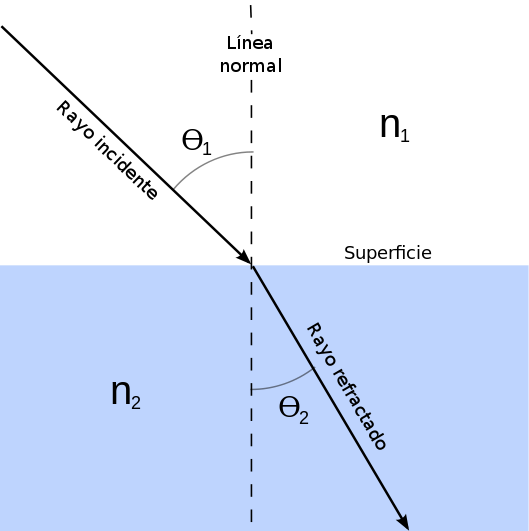
La fórmula de la Ley de Snell es la siguiente:
n1 seni = n2 senr
Siendo i y r el ángulo de incidencia y el ángulo refractado respectivamente.
Demostración de la Ley de Snell
Para conocer la demostración de la fórmula de la Ley de Snell debemos conocer antes las leyes de la refracción:
- El rayo de incidencia, la normal a la superficie en el punto de incidencia y el rayo refractado se encuentran en el mismo plano.
- La razón entre el seno de ángulo de incidencia (i) y el del ángulo de refracción (r) es una constante que equivale a la razón entre las respectivas velocidades de propagación del movimiento ondulatorio. Esto se puede expresar matemáticamente mediante la siguiente fórmula:
seni/senr = v1/v2
Una vez que conocemos las leyes de la refracción por las cuales se rige la Ley de Snell, podemos pasar a hablar del índice de refracción relativo. Este concepto es el cociente de dividir los índices de refracción de los medios.
Por ejemplo, el índice de refracción relativo del medio 2 con respecto del medio 1 es este:
n21 = n2 / n1
Mientras que el índice de refracción relativo del medio 1 con respecto del medio 2 sería este otro:
n12 = n1 / n2
Si relacionamos la fórmula del índice de refracción relativo con la segunda ley de la refracción, tenemos que:
n21 = n2 / n1 = v1 / v2 = seni / senr
De ahí se deduce la expresión de la Ley de Snell, quedando demostrada su fórmula:
n1 seni = n2 senr
Índice de refracción
Hemos hablado en varias ocasiones del índice de refracción pero, ¿qué es exactamente?. El índice de refracción es un número que nos indica la relación existente entre la velocidad de la luz en el vacío (c) y la velocidad (v) de propagación en dicho medio. Esto se puede expresar matemáticamente con la siguiente fórmula:
n = c/v
En el vacío o en el aire, el índice de refracción es igual a 1. En el resto de medios, el n es mayor que uno ya que la velocidad de la luz (c) siempre va a ser mayor que la velocidad de propagación en ese medio.
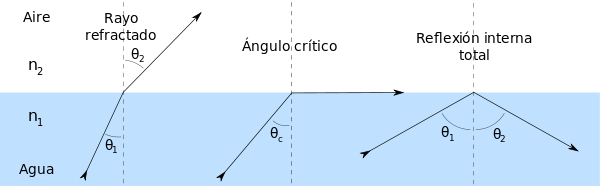
Ángulo límite y reflexión total
Hay un fenómeno llamado reflexión total y que ocurre cuando la luz pasa de un medio a otro con índice de refracción menor, dando como resultado que se refracte alejándose de la normal.
A medida que aumentamos el ángulo de incidencia, el ángulo refractado también aumenta hasta que llega un punto a partir del cual, la luz se refleja totalmente y se produce el fenómeno de la reflexión total.
Para saber cuál es ese punto a partir del cual se produce la reflexión total, se establece un ángulo límite en el que el ángulo de refracción es igual a 90º. Esta es la fórmula para conocer cuál es el ángulo límite (L):
senL = n2/n1
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.