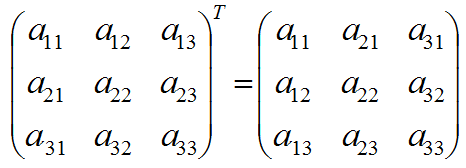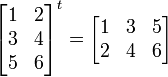La calculadora de matriz transpuesta online es una herramienta que te permite intercambiar filas por columnas de una matriz de forma automática. Sólo tienes que seleccionar el tamaño de la matriz entre los tamaños que tenemos disponibles y pulsar el botón de Calcular para conocer la transpuesta de esa matriz.
Si quieres saberlo todo sobre la matriz transpuesta, sigue leyendo y te contaremos todo sobre este tipo de matriz tan utilizada en el mundo de las matemáticas, física y otras disciplinas.
Contenido de este artículo
Qué es una matriz transpuesta
La transpuesta de una matriz es aquella en la que se han intercambiado filas por columnas. Se trata de una operación que no requiere ningún cálculo adicional por lo que es una operación que nos llevará sólo unos segundos.
Cabe destacar que cuando transponemos una matriz, añadimos una pequeña T en la parte superior derecha, de tal forma que visualmente se puede ver de esta forma (A)t.
Cómo hacer una matriz transpuesta
Tal y como hemos visto en el punto anterior, hacer una matriz transpuesta consiste en cambiar filas por columnas. Para que quede más claro, vamos a verlo con un ejemplo práctico como el siguiente:
La única dificultad que entraña calcular la matriz transpuesta es no equivocarse a la hora de cambiar las filas por columnas y que equivoquemos algún número. Por lo demás, es muy fácil de hacer.
Propiedades de la matriz transpuesta
A continuación encontrarás las principales propiedades de la matriz transpuesta para que las tengas en cuenta a la hora de resolver problemas matemáticos con ellas:
- (At)t=A: esto quiere decir que si transponemos una matriz transpuesta, nos quedamos con la matriz de partida.
- (A + B)t = At + Bt : la transpuesta de la suma de matrices es igual a la suma de la matriz transpuesta de cada una de las matrices.
- (AB)t = BtAt: la transpuesta del producto de dos matrices es igual al producto de la matriz transpuesta de cada una de las matrices.
- (rA)t = rAt: si un número escalar multiplica a una matriz, el orden en el que hacemos la matriz transpuesta es irrelevante ya que obtendremos el mismo resultado.
Matriz transpuesta en Excel
Hay dos formas de transponer una matriz en Excel aunque dependiendo de cual escojamos, tendremos un resultado referenciado o no.
¿Qué quiere decir esto? Que si escogemos la forma no referenciada, cuando hagamos cambios en la matriz, la transpuesta no tendrá esos cambios aplicados de forma instantánea mientras que de la otra forma, todas las modificaciones que hagamos se verán automáticamente en la matriz transpuesta.
Vamos a ver cómo se hace cada uno.
Matriz transpuesta no referenciada
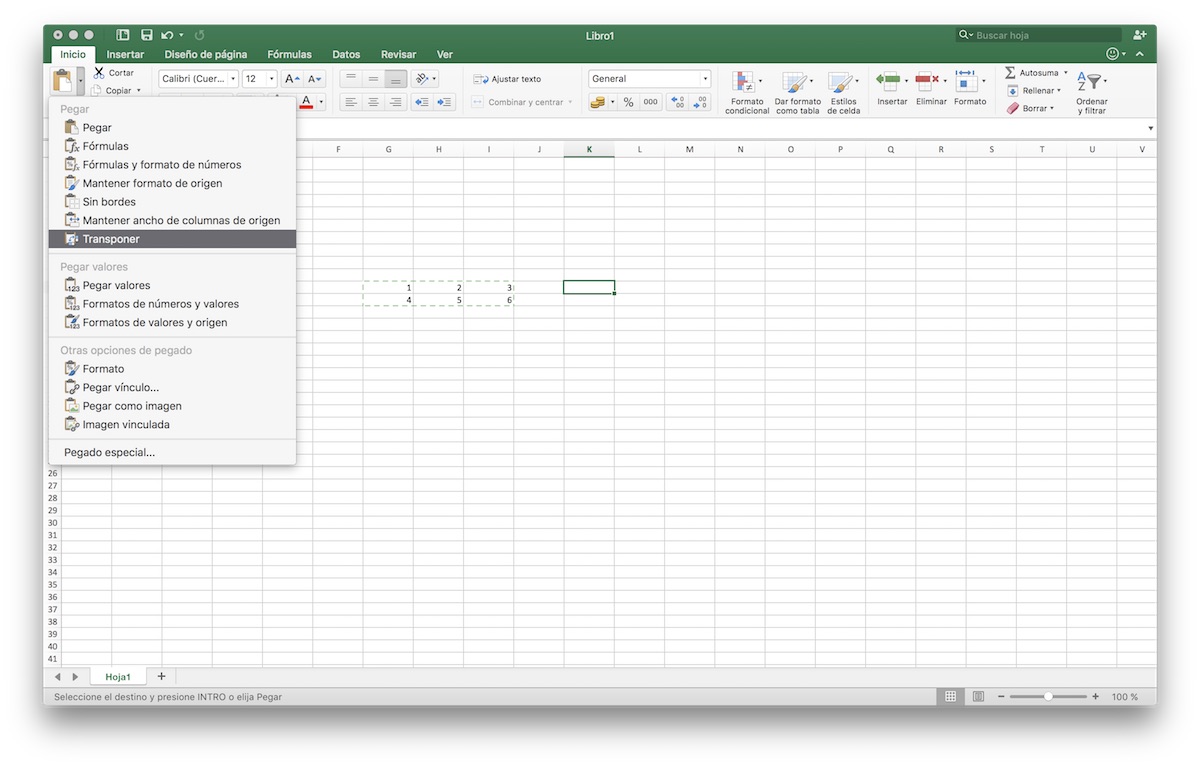
En este caso, sólo tenemos que escribir los elementos de la matriz, seleccionar el rango de datos y los copiamos en el portapapeles (CTRL+C ó CMD+C si usas Mac).
A continuación, selecciona una celda vacía de la hoja de cálculo, vete a las opciones de pegar y selecciona la opción de "Transponer". Tras pulsarla, verás que los datos se han transpuesto.
La pega de este método es que si modificamos la matriz original, la transpuesta no se modifica. Para solucionar esto, vamos a ver el método referenciado a continuación.
Función de Transponer en Excel
Este segundo método es el que nos permite transponer datos en Excel de forma automática y vinculante, para que si hacemos cambios en la matriz original, la transpuesta también tenga esos cambios aplicados al momento.
Para ello, escribe los elementos de la matriz y cuando lo hayas hecho, busca un rango de celdas en blanco que coincida con el número de celdas que hay en el conjunto original. Es decir, que si tenemos una matriz original de 2x4 celdas, debemos seleccionar un rango de 4x2 celdas para que se aplique la función de transponer correctamente.
Cuando tengas ese rango de celdas vacías seleccionado, escribe la siguiente función asegurándote de que entre los paréntesis, has seleccionado el rango de datos en los que se encuentra la matriz de partida.
=TRANSPONER()
A continuación, pulsa en tu teclado las teclas CTRL+MAYÚSCULAS+INTRO y verás que aparece en Excel la matriz transpuesta.
Determinante de una matriz transpuesta
El determinante de una matriz es igual al determinante de su transpuesta de tal forma que:
Determinante de (A) = Determinante (A)t
Es importante que recuerdes que sólo se puede calcular el determinante de matrices cuadradas, es decir, cuyo número de filas es igual al número de columnas. Si quieres, aquí puedes saber más sobre cómo calcular los siguientes tipos de determinantes:
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.