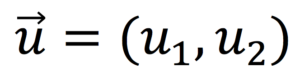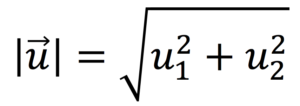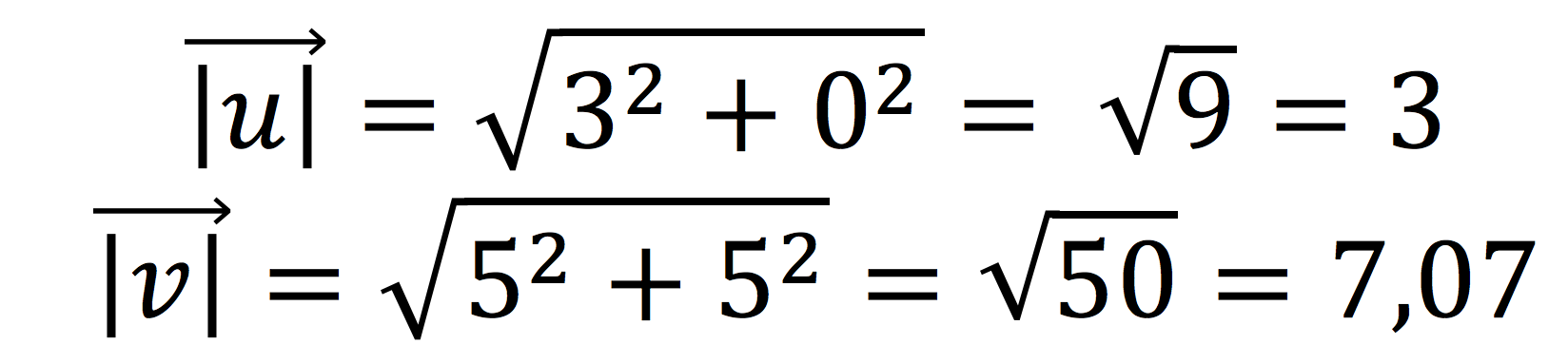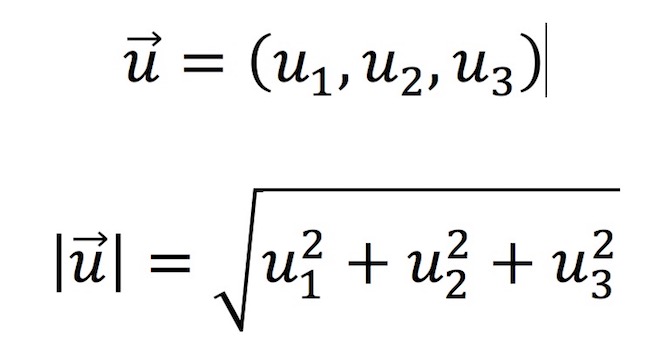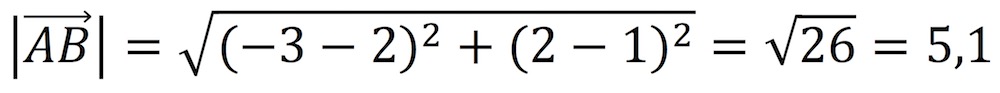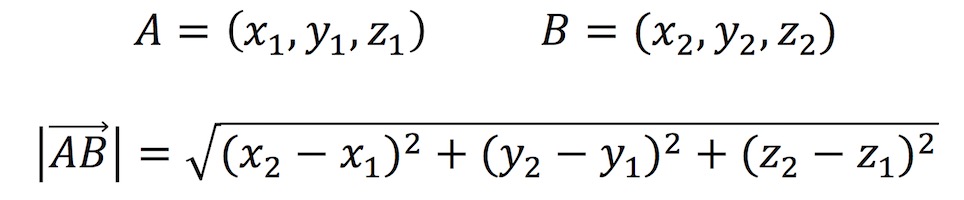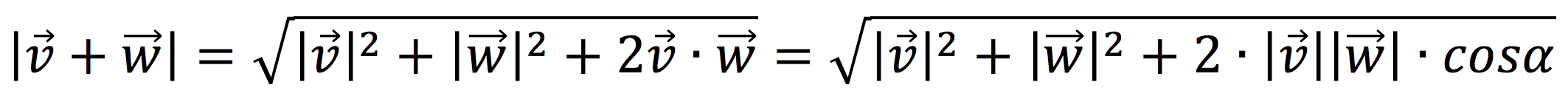Calcular el módulo de un vector es una operación que tendrás que utilizar en numerosos ejercicios de matemáticas, como por ejemplo, el cálculo del producto escalar de dos vectores. A continuación tienes una calculadora que te permite obtener el módulo de un vector a partir de sus componentes (v1, v2) o de la posición de dos de sus puntos A (x1, y1) y B (x2, y2)
Sólo tienes que escribir en nuestra calculadora los datos del vector que conozcas y pulsar el botón de calcular para obtener su módulo. Además, si quieres aprender a calcular el módulo de un vector te enseñamos cómo se hace.
Contenido de este artículo
¿Qué es el módulo de un vector?
Cuando hablamos del módulo de un vector nos estamos refiriendo a la longitud del segmento que se encuentra entre sus extremos A y B:
Cuando calculemos el módulo, siempre obtendremos un valor positivo o igual a cero si se trata de un vector nulo.
Cómo calcular el módulo de un vector con sus componentes
Un vector está definido por sus componentes y a partir de ellas podemos calcular su módulo aplicando la siguiente fórmula:
Básicamente lo que tienes que hacer es calcular la raíz cuadrada de la suma de cada componente elevada al cuadrado.
Por ejemplo, vamos a calcular la raíz cuadrada de dos vectores = (3, 0) y
= (5, 5):
Si el vector es tridimensional, es decir, tiene tres componentes, la fórmula para calcular su módulo es exactamente la misma pero añadiendo el cuadrado de esa tercera componente. Es decir, tendrías que aplicar esta ecuación:
En el caso de un vector en R3, calcularemos la raíz cuadrada de la suma de las componentes x, y, z elevadas al cuadrado.
Calcular el módulo de un vector a partir de las coordenadas de dos puntos
Existe un segundo método para sacar el módulo de un vector a partir de las coordenadas de dos de sus puntos. Sólo tenemos que aplicar la siguiente fórmula:
Como ejercicio resuelto, vamos a calcular el módulo de un vector cuyos puntos son A(2, 1) y B(-3, 2). Aplicamos la fórmula que tenemos justo en la imagen que está encima de estas líneas y nos queda que:
¿Y cómo se calcula si las coordenadas son tridimensionales? En el caso de que cada uno de los puntos del vector tenga coordenadas x, y, z, entonces la fórmula a usar es esta:
El proceso es exactamente el mismo que en el caso bidimensional aunque en la ecuación se tiene en cuenta esa tercera coordenada del eje Z.
Módulo de la suma de dos vectores
Para calcular el módulo de la suma de dos vectores tenemos que:
- Calcular el cuadrado del módulo de cada vector
- Calcular el producto escalar de los dos vectores
Cuando lo tengamos, aplicamos la siguiente fórmula matemática:
Si te ha quedado alguna duda de cómo sacar el módulo de un vector a partir de sus componentes o de sus coordenadas, déjanos un comentario y estaremos encantados de ayudarte.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.