¿Necesitas una calculadora para pasar de forma polar a binómica o de binómica a polar? Aquí tienes una herramienta dedicada a los números complejos junto con mucha más información para que conozcas las propiedades, operaciones y mucho más.
Para cambiar un número de polar a binómica o viceversa sólo tienes que seleccionar el cambio que quieres hacer en nuestra calculadora, escribir los valores que correspondan en cada caso y pulsar el botón de calcular para obtener la equivalencia automáticamente.
Contenido de este artículo
¿Qué es un número complejo?
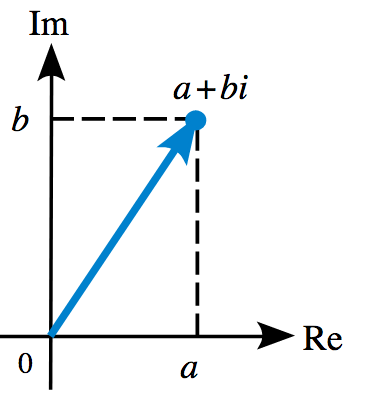
Un número complejo es una extensión de los números reales y están compuestos por una parte real y una imaginaria. Los complejos pueden representarse en forma binómica o en forma polar:
- Forma Binómica: se escriben de la forma z = a + bi, siendo a la parte real y b la imaginaria.
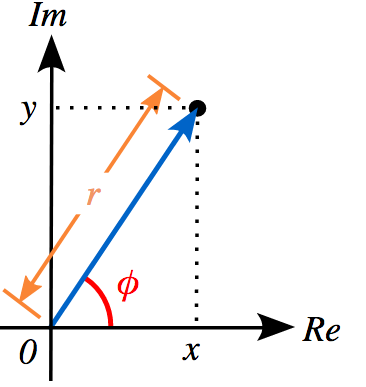
- Forma polar: se representan como z= rα, siendo r el módulo y α el argumento.
¿Y para qué se usan los números complejos? La respuesta es larga pero a modo de resumen podemos decir que los usamos para resolver operaciones que no tienen solución real (como la raíz cuadrada de un número negativo).
Así es como surge la unidad imaginaria que se representa con la letra i y que equivale a la raíz cuadrada de - 1, es decir:
i = √-1
Pasar de forma polar a binómica
Para pasar un número complejo de forma polar a binómica, tenemos que aplicar la siguiente fórmula matemática:
z = rα = r (cos α + i sen α)
Por ejemplo, si queremos pasar a binómica el complejo 3240º, aplicaremos la fórmula de la siguiente forma:
z = 3240º = 3 (cos 240º + i sen 240º) = 3 (-0,5 - 0,866i) = -1,5 - 2,598i
Si te sirve de utilidad, aquí te dejamos las correspondientes calculadoras para sacar el seno y el coseno.
Convertir de binómica a polar
Si queremos hacer la conversión inversa, es decir, pasar un número complejo de coordenadas cartesianas a polares, entonces tenemos que realizar el siguiente proceso:
- Lo primero será calcular el módulo del número complejo (z = a + bi), para lo cual aplicamos esta fórmula:
|z| = √(a2 + b2)
- Ahora tenemos que obtener el argumento de las coordenadas polares, que lo obtenemos con esta fórmula:
α = arctg (b/a)
Te dejamos con nuestra calculadora de arcotangente para resolver la operación anterior de forma inmediata.
Vamos a proponer un ejercicio resuelto en el que vamos a pasar a polares el complejo 1 + 2i.
|z| = √(12 + 22) = √(1 + 4) = √5
α = arctg (b/a) = arctg (2/1) = 63,43º
Finalmente tenemos que nuestro número complejo 1 + 2i en coordenadas cartesianas se expresa como √563,43º en coordenadas polares
Operaciones
A continuación os vamos a enseñar cuáles son las principales operaciones que se pueden hacer con los números complejos.
Ten en cuenta que algunas de estas operaciones sólo se pueden realizar en forma binómica o en polar, por lo que necesitarás pasar de un formato a otro dependiendo de cómo esté expresado el número complejo que tengas.
Suma y resta de números complejos
La suma o resta de números complejos en forma binómica es muy sencilla. Sólo tenemos que sumar las partes reales y las partes imaginarias como se puede ver en la siguiente expresión:
(a+bi)+(c+di) = (a+c)+(b+d)i
(a+bi)−(c+di) = (a−c)+(b−d)i
Por ejemplo:
(3 + 2i) + (1 + 5i) = (3 + 1) + (2 + 5)i = 4 + 7i
(4 + 3i) - (2 + 1i) = (4 - 2) + (3 - 1)i = 2 + 2i
Propiedades de la suma
- Propiedad conmutativa: z1 + z2 = z2 + z1
- Propiedad asociativa (z1 + z2) + z3 = z1 + (z2 + z3)
- El 0 es el elemento neutro
Multiplicación de números complejos
Multiplicar números complejos lo podemos hacer tanto en forma polar como en forma binómica. Vamos a ver cómo se realiza en cada caso:
Producto de números complejos en forma binómica:
(a+bi)·(c+di) = (a·c − b·d)+(a·d+b·c)i
Ejercicio resuelto:
(1 + 3i)·(2+1i) = 1·2 - 3i2 + 1i + 6i = 2 - 3 + i + 6i = -1 + 7i
Recuerda que i2 es igual a -1
Producto de números complejos en forma polar:
mα·m'β=(m·m')α+β
Ejemplo resuelto:
230º · 535º = (2 · 5)30º+35º = 1065º
Propiedades de la multiplicación:
- Propiedad conmutativa: z1 · z2 = z2 · z1
- Propiedad asociativa: (z1 · z2) · z3 = z1 · (z2 · z3)
- Propiedad distributiva: z1 · (z2 + z3) = z1 · z2 + z1 · z3
- El 1 es el elemento neutro (1 + 0i)
División de números complejos
La división es otra de las operaciones que nos permite trabajar tanto en forma binómica como polar. Vamos a ver cómo se procede en cada una de ellas:
División de números complejos en forma binómica
Si tenemos dos números complejos expresados en forma binómica, la forma de dividirlos es la siguiente:
Si te interesa saber cómo se llega a esa expresión, a continuación tienes la demostración en la que se ha multiplicado al numerador y al denominador por el conjugado del denominador, así obtenemos un número real en esa parte de la fracción:
División de números complejos en forma polar
Para dividir complejos en forma polar simplemente hay que dividir el módulo y restar los argumentos como indica la siguiente fórmula:
Potencias de números complejos
En el caso de que tengamos que calcular la potencia de un número complejo, a continuación te explicamos cómo calcularla en cada caso:
Potencia de un número complejo en forma binómica
Esta es la fórmula a desarrollar n veces para calcular la potencia de un número complejo en forma binómcia:
Dependiendo de la complejidad, quizás te sea más fácil convertir el número complejo a forma polar y calcular la potencia como te indicamos en el siguiente punto.
Potencias de un número complejo en forma polar
En mi opinión, calcular potencias en forma polar es mucho más fácil que en forma binómica ya que sólo tenemos que aplicar la siguiente fórmula:
(mα)n = mnnα
Como puedes ver, sólo tienes que elevar el módulo a la potencia n y multiplicar al argumento por el valor de n.
Módulo de un número complejo
Si quieres más información de cómo se calcula el módulo de un número complejo, entra en el link que te acabamos de dejar.
Conjugado de un número complejo
El conjugado de un número complejo en forma binómica es aquel que tiene la misma parte real y cambiada de signo la parte imaginaria, de tal forma que si nuestro complejo es Z = a + bi, su conjugado será:
Propiedades del conjugado de un número complejo
Estas son las propiedades que tiene un número complejo:
- El conjugado de un número real es él mismo. Por ejemplo, el conjugado de 3 +0i es igual a 3 -0i, en definitiva, es 3 en ambos casos.
- El conjugado de un número imaginario puro es su opuesto. Por ejemplo: el conjugado de 5i es -5i
- El conjugado del conjugado es el número imaginario inicial.
- La suma de un número complejo más su conjugado es igual a dos veces su parte real:
- La resta de un complejo menos su conjugado es igual a dos veces su parte imaginaria:
- El producto de un complejo por su conjugado es igual al cuadrado de la parte real más el cuadrado de la parte imaginaria:
- Para la suma y el producto de varios conjugados se cumple que:
Números complejos en Excel
Excel tiene numerosas funciones destinadas a operar con números complejos. A continuación te dejamos una tabla que te servirá como resumen para ver cuáles son y qué es lo que hacen.
Si alguna no sabes cómo se utiliza o para qué sirve, no dudes en dejarnos un comentario y te ayudaremos a cualquier cosa que tenga que ver con los números complejos.
| Función | Descripción |
|---|---|
| COMPLEJO | Convierte coeficientes reales e imaginarios en un número complejo. |
| IM.ABS | Calcula el módulo de un complejo. |
| IM.ANGULO | Calcula el ángulo del argumento (en radianes) |
| IMAGINARIO | Nos da el coeficiente de la parte imaginaria |
| IM.CONJUGADA | Calcula el conjugado de un complejo |
| IM.COS | Nos da el coseno de un número complejo. |
| IM.DIV | La usaremos para dividir dos números complejos |
| IM.EXP | Nos permite calcular la forma exponencial de un complejo |
| IM.LN | Devuelve el logaritmo neperiano de un número complejo. |
| IM.LOG10 | Nos aporta el logaritmo en base 10 del complejo |
| IM.LOG2 | Esta función nos calcula el logaritmo en base 2. |
| IM.POT | Nos ayuda a calcular la potencia de un complejo |
| IM.PRODUCT | Nos permite multiplicar hasta 29 números complejos |
| IM.RAIZ2 | La usaremos para sacar la raíz cuadrada del complejo |
| IM.REAL | Nos da la parte real del número complejo |
| IM.SENO | Con esta función calculamos el seno de un número complejo |
| IM.SUM | El resultado será la suma de dos números complejos |
| IM.SUSTR | Esta función se usa para restar dos números complejos |
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.

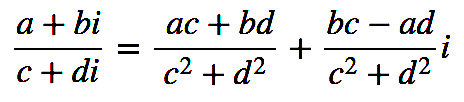
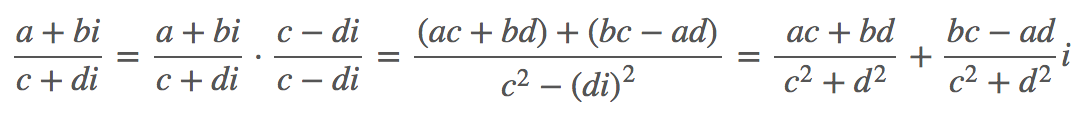
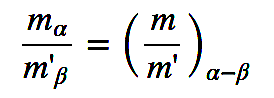
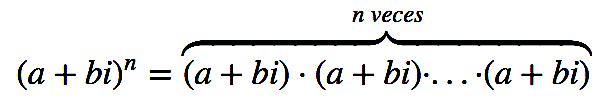
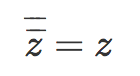
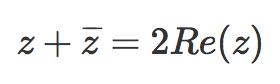
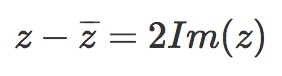
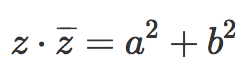
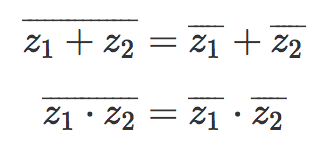
Estaba usando la calculadora para conversión de números complejos, sin embargo considero que debe estar en revisión la ejecución de los cálculos, en su defecto debe de revisarse, coloque el siguiente vector: -3i -3j, dando como resultado, modulo complejo 4,2426 (argumento 45grados). Cuando realizas la demostración grafica este vector se representa con el siguiente valor ( modulo complejo 4.24 (argumento 225 grados «O» -135grados).
Resumen:
vector Resultado por su Calculadora Resultado Verdadero
(-3i -3j ) 4.24 (ar 45grados) 4.24 (ar (-135) o (225) grados