¿Tienes que calcular la pendiente de una recta? Usa nuestra calculadora y obtendrás tanto la pendiente como la ecuación de la recta que pasa por dos puntos.
Sólo tienes que escribir las coordenadas de cada punto (x1, y1) (x2, y2) y pulsar el botón de calcular para obtener todos los datos de la recta que forman.
Contenido de este artículo
¿Qué es la pendiente de una recta?
La pendiente se define como el grado de inclinación de un elemento. Desde el punto de vista geométrico, la pendiente mide la inclinación de la recta con respecto al eje de abscisas o eje X.
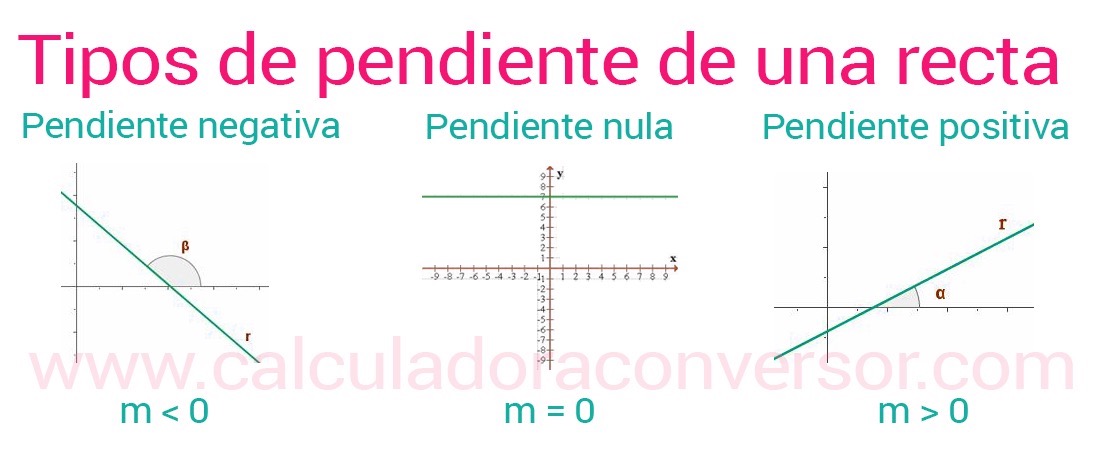
La pendiente de una recta se representa con la letra m y puede ser de distintos tipos:
- Positiva: la recta es ascendente y el ángulo que forma la recta con el eje x es agudo. Si el ángulo crece, la pendiente también lo hace. En este caso, el valor de m siempre es positivo.
- Negativa: en este caso la recta es descendente y el ángulo formado de la recta con el eje X es obtuso. Si el ángulo crece, la pendiente decrece. Por último, en caso de tener pendiente negativa, los valores de m serán negativos.
- Pendiente nula o igual a cero: En estos casos en los que m = 0 podemos observar como la recta es paralela al eje X y, por lo tanto, no tiene pendiente. En definitiva, es completamente horizontal.
Cómo calcular la pendiente si nos dan el ángulo
Si nos dan el ángulo que forma la recta con el eje X, podemos calcular la pendiente aplicando la siguiente fórmula:
m = tan θ
Simplemente tenemos que calcular la tangente del ángulo. Como hemos dicho antes, si el ángulo es:
- Agudo (menos de 90º): la pendiente es positiva y crece a medida que aumenta su valor.
- Obtuso: (más de 90º): la pendiente es negativa y disminuye a medida que aumenta su valor.
Vara demostrarlo, vamos a calcular la pendiente de un ángulo de 30º y otra de 100º para verificar si lo anterior es cierto:
m = tan 30º = 0,57
m = tan 100º = -5,67
Efectivamente, confirmamos que dependiendo del tipo de ángulo que forme la recta con el eje X, el valor de la pendiente puede ser negativo o positivo.
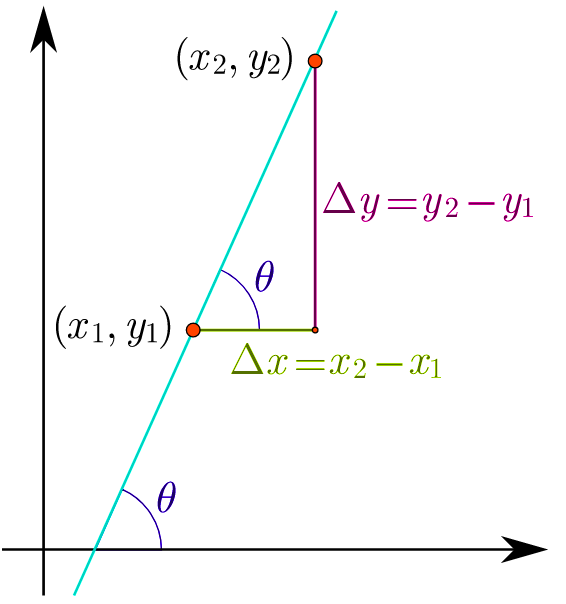
Fórmula para calcular la pendiente que pasa por dos puntos
Si queremos calcular la pendiente de una recta que pasa por dos puntos, tenemos que aplicar la fórmula que tenéis encima de estas líneas.
Simplemente hay que calcular el cociente del incremento del eje y entre el incremento que hay en el eje x. Para entenderlo mejor, vamos a ver un ejercicio resuelto en el que nos piden calcular la pendiente de una recta que pasa por los puntos (3,4) y (1,2).
Aplicamos la fórmula y tenemos que:
m = (2 - 4) / (1 - 3) = -2/-2 = 1
Obtener la pendiente dado el vector director de la recta
El vector director de una recta se define como el vector que se encuentra en dicha recta o es paralelo a ella. Esto quiere decir que del vector director lo que realmente nos interesa es su dirección.
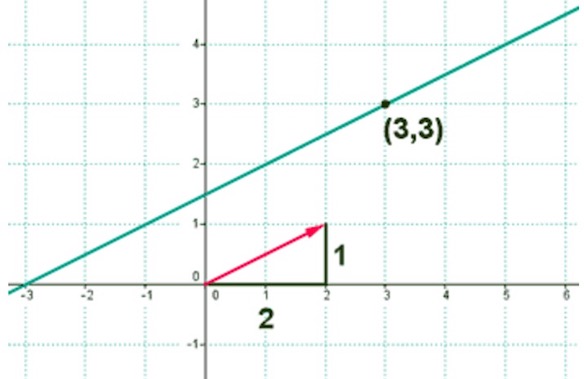
Por ejemplo, el vector director (2, 1) quiere decir que por cada dos unidades del eje x, aumentamos una unidad en el eje y. Además, como es paralelo o se encuentra dentro de la propia recta, la pendiente será la misma.
¿Cómo calculamos la pendiente en este caso? Simplemente tenemos que calcular este cociente:
m = v2 / v1
En el caso del ejemplo, la pendiente sería:
m = 1 /2 = 2
Sacar la pendiente si nos dan la ecuación de la recta
Cuando nos dan la ecuación de la recta, podemos calcular la pendiente de distintas formas. Todo depende de cómo sea la ecuación de la recta, así que vamos a ver los casos más comunes y cómo se saca la pendiente en cada uno de ellos.
Con la ecuación continua de la recta
Por ejemplo, si nos dan la ecuación punto-pendiente o ecuación continua de la recta:
La pendiente será m = v2 / v1
Con la ecuación punto-pendiente de la recta
En este caso, la fórmula puede ser este tipo:
y - y1 = m (x - x1)
y = mx + n
En ambos casos, la pendiente es el valor de m.
Con la ecuación general de la recta
Si nos dan la ecuación general de la recta (Ax + By + C = 0), podemos calcular la pendiente con la siguiente ecuación:
m = - A/B
Calcular la pendiente de una recta con Excel
¿Sabes que puedes calcular la pendiente de una recta en Excel? Sólo necesitas conocer al menos dos puntos de la recta para poder hacerlo.
Si los conoces, abre una nueva hoja de cálculo y escribe en cada celda las coordenadas de cada punto.
Cuando hayas puesto los puntos de la recta, escribe en Excel la siguiente función:
=PENDIENTE(coordenadas_y;coordenadas_x)
Siendo coordenadas_y y coordenadas_x los intervalos de las celdas en los que has escrito las posiciones de los puntos.
Para que quede mejor explicado vamos a ver un ejemplo práctico en el que vamos a calcular la pendiente de una recta que pasa por los puntos (1,3) y (5,6). Los escribimos en Excel y nos quedará algo así:
Ahora aplicamos la función de Excel que hemos visto un poco más arriba y quedaría así:
=PENDIENTE(B2:B3;A2:A3)
Como ves, en el intervalo B2:B3 hemos escrito las coordenadas y de los puntos de la recta y en el intervalo A2:A3 tenemos las coordenadas del eje x.
Si después de nuestro post con la teoría para calcular la pendiente de una recta sigues teniendo dudas, déjanos un comentario y te ayudaremos lo antes posible.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.
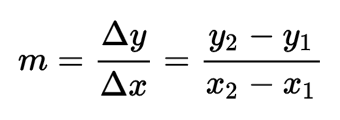

Valioso rigor conceptual, importantes y útiles herramientas mediadoras para la adquisición de resultados virtuales. Gracias.