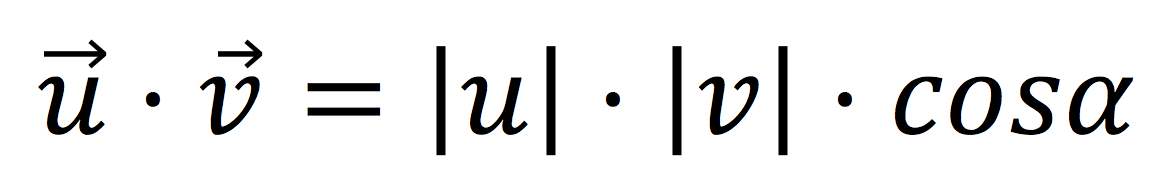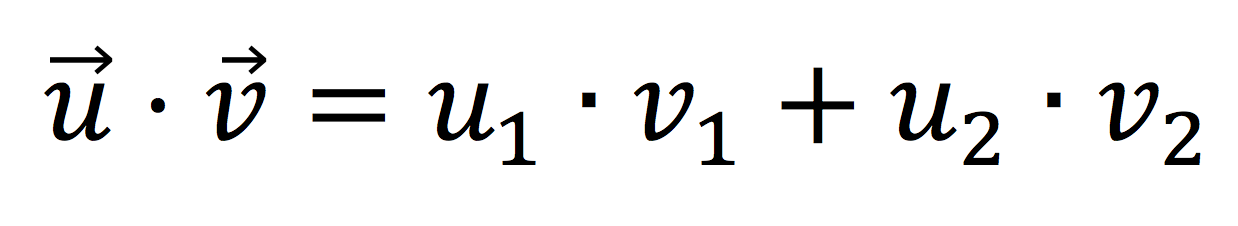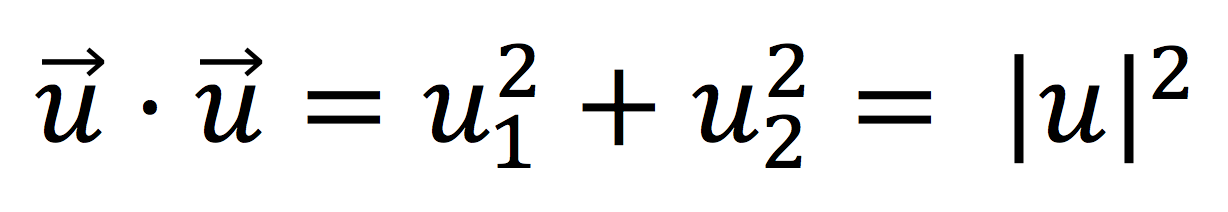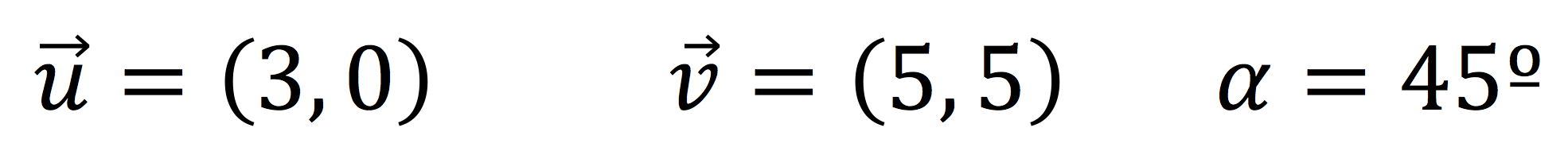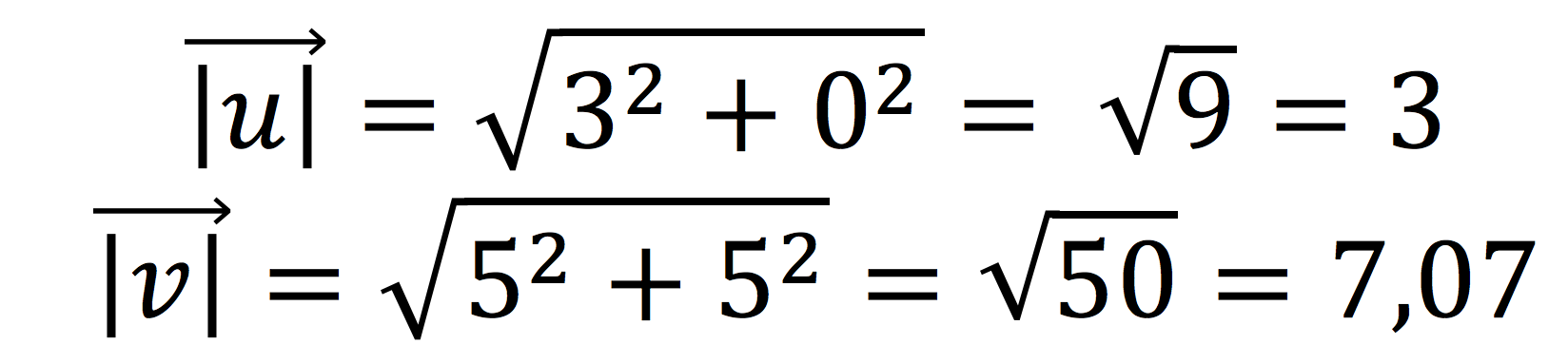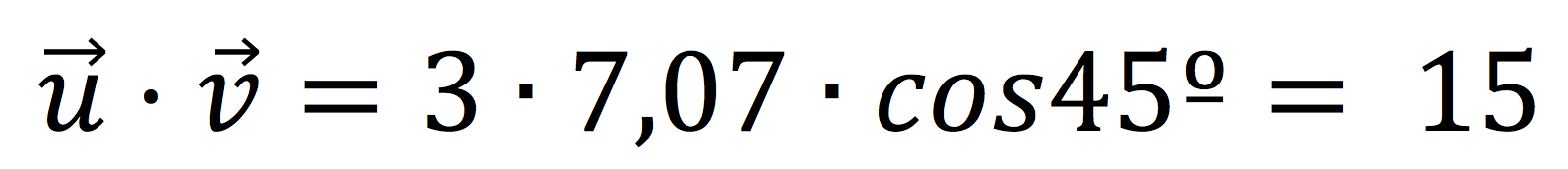¿Tienes que calcular el producto escalar de dos vectores? Descubre cómo se hace aquí o usa nuestra calculadora online para conocer el resultado de forma inmediata.
Sólo necesitas escribir las componentes del vector y las del vector
así como el ángulo que forman los dos vectores en grados. Pulsa el botón de calcular y automáticamente conocerás su producto escalar.
Contenido de este artículo
Fórmula del producto escalar de dos vectores
Para calcular el producto escalar de dos vectores tienes que aplicar la siguiente fórmula matemática:
dónde:
- |u| y |v| son el módulo de cada vector (averigua aquí cómo se calcula el módulo de un vector).
- cosα es el coseno del ángulo que forman los dos vectores.
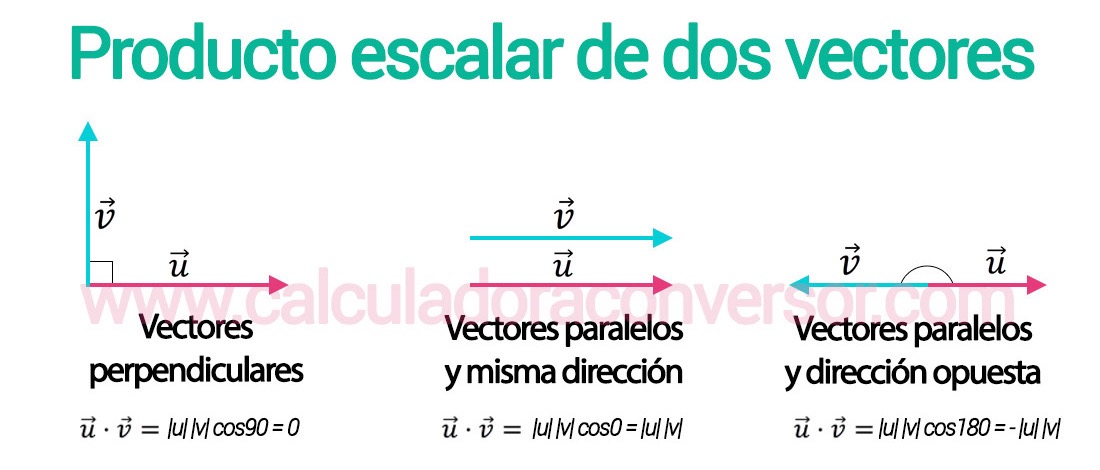
Dependiendo de cómo sea ese ángulo α, la fórmula anterior se puede simplificar en determinados casos:
- Si los vectores son perpendiculares (α = 90º), el producto escalar será cero. Esto se debe a que el coseno de 90 es igual a 0.
- Si los vectores son paralelos y tienen el mismo sentido (α = 0º), la fórmula se reduce al producto de los módulos |u|⋅|v| Esto se debe a que el coseno de 0 es igual a 1.
- Si los vectores son paralelos pero tienen sentido opuesto (α = 180º), la fórmula será del producto escalar será - |u|⋅|v|. Ese símbolo negativo se debe a que el coseno de 180 es igual a -1.
Hay que tener en cuenta que el producto escalar de dos vectores nos dará como resultado un número real. También es muy importante que no lo confundas con el producto vectorial.
Fórmula analítica del producto escalar
Cuando calculamos el producto escalar de dos vectores desde el punto de vista analítico, obtenemos como resultado un número escalar que es el resultado de multiplicar cada una de las componentes cartesianas de los dos vectores según podemos ver en esta fórmula:
Producto escalar de un vector por si mismo
La fórmula anterior nos vendrá muy bien para hacer un ejercicio resuelto en el que vamos a calcular el producto escalar de un vector por si mismo.
Como puedes ver, el producto escalar de un vector por si mismo es igual al cuadrado de su módulo. También hubiésemos podido resolver el ejercicio aplicando la fórmula general del producto escalar y poniendo α = 0º.
El producto escalar de un vector por sí mismo siempre va a ser positivo (siempre y cuando sea un vector no nulo)
Propiedades del producto escalar
A la hora de resolver ejercicios, te vendrá bien conocer las propiedades del producto escalar:
- Conmutativa: u ⋅ v = v ⋅ u
- Distributiva (suma vectorial): x ⋅ (u + v) = x ⋅ u + x ⋅ v
- Asociativa (producto por un escalar m): m (u ⋅ v) = (mu) ⋅ v = u ⋅ (mv)
Ejercicios resueltos
A continuación vamos a ver un par de ejercicios en los que vamos a calcular el producto escalar de los siguientes vectores:
Lo primero que vamos a hacer va a ser calcular el módulo de cada vector:
Ahora aplicamos la fórmula general y nos queda que:
Si quieres practicar con más ejercicios resueltos, invéntate los datos de dos vectores y usa nuestra calculadora para comprobar el resultado. Si en alguno tienes problemas, escríbenos un comentario y te ayudaremos.
Calcular producto escalar de dos vectores en Excel
Como no podía ser de otra forma, Excel también tiene una función que nos permite calcular el producto escalar de dos vectores mediante la fórmula analítica.
Esta función no se encuentra fácilmente en el programa de Microsoft así que os vamos a explicar cómo se hace. Lo primero que tienes que realizar es abrir una nueva hoja de cálculo y usar una celda vacía para escribir cada componente del vector. Nosotros vamos a calcular el producto escalar de los vectores (-1, 3) y (2, -2) así que nos ha quedado de esta forma:
Ahora usaremos la función SUMAPRODUCTO para obtener el producto escalar. En nuestro caso del ejemplo, nos ha quedado así:
=SUMAPRODUCTO(B2:C2;B3:C3)
Fíjate que en el intervalo de celdas B2:C2 están las componentes del vector 1 y en el rango B3:C3 las del vector 2. Tendrás que adaptar estos rangos a las celdas que hayas usado tú.
Ahora simplemente tienes que pulsar la tecla INTRO y Excel te calculará automáticamente el producto escalar de esos dos vectores usando la fórmula analítica.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.