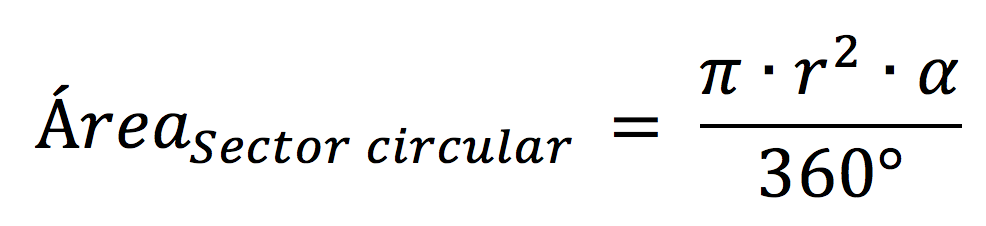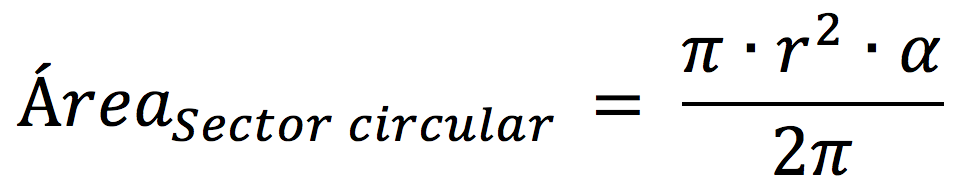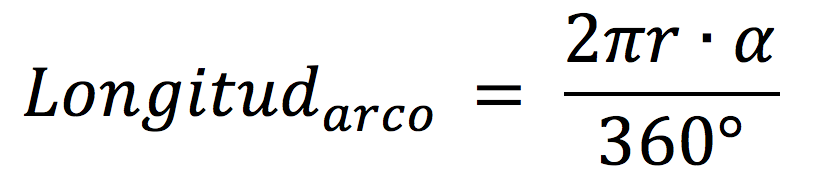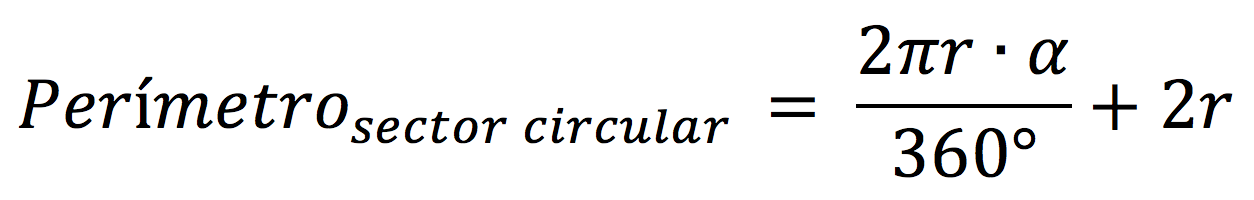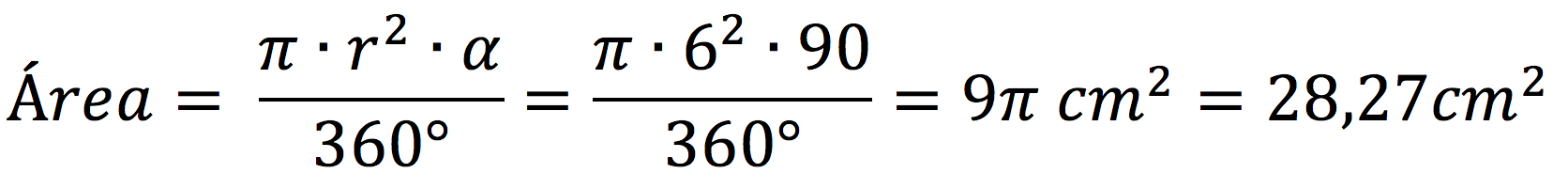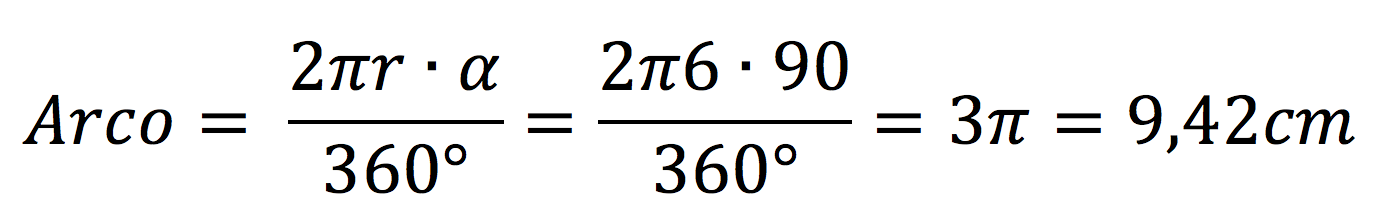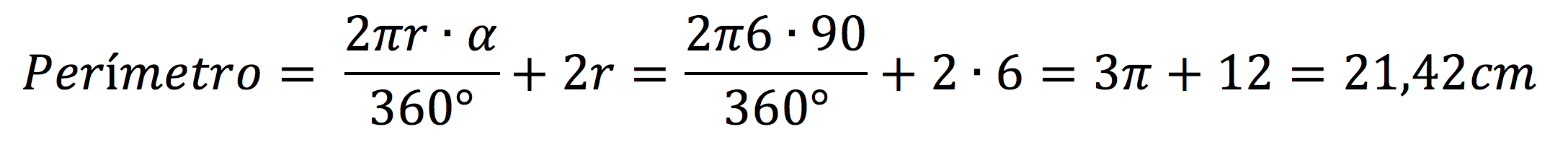¿Quieres calcular el área de un sector circular? Usa nuestra calculadora online y obtendrás la superficie del sector automáticamente así como su longitud del arco y perímetro.
Sólo necesitas saber el radio del círculo (r) y el número de grados (α) que ocupa dicho sector circular. Cuando lo tengas, pulsa el botón de calcular y obtendrás el resultado inmediatamente.
Contenido de este artículo
¿Qué es un sector circular?
Cuando queremos calcular el área de un círculo, lo hacemos teniendo en cuenta toda su superficie. Sin embargo, puede que nos interese solamente una porción del círculo por lo que a dicha porción la denominamos sector circular.
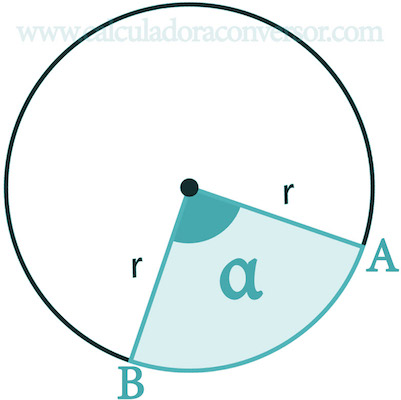
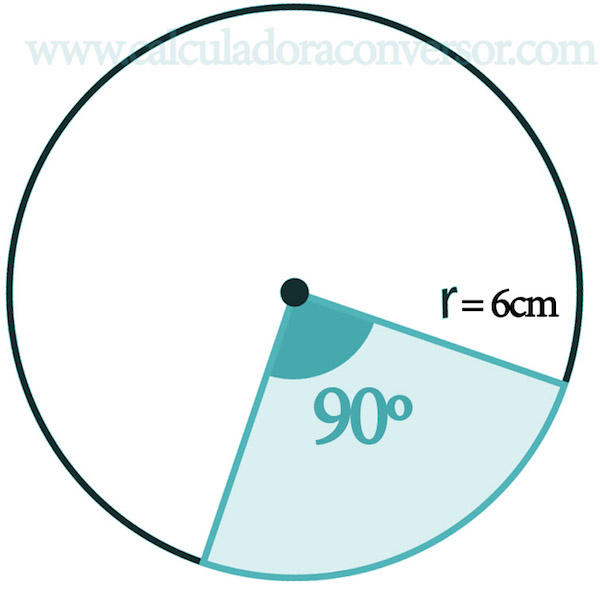
Si nos fijamos en la figura que hay encima de estas líneas, el sector circular correspondería a la parte coloreada en turquesa. Se forma por la rotación del radio una cantidad determinada de grados o radianes.
Área de un sector circular
Ahora que ya sabemos qué es un sector circular, vamos a aprender cómo calcular su área. Para ello, usaremos la siguiente fórmula matemática:
En dicha fórmula tenemos dos incógnitas que debemos conocer:
- r es el radio del círculo
- α es el ángulo en grados del sector
Si nos diesen el ángulo del sector expresado en radiantes tenemos dos opciones. La primera de ellas es pasar de radianes a grados mientras que la segunda opción es aplicar esta otra fórmula:
Recuerda: esta segunda fórmula para calcular el área del sector circular la usaremos si nos dan el ángulo expresado en radianes.
Longitud del arco
Si nos piden calcular la longitud del arco del sector circular, se refieren a la distancia que hay desde el punto A al punto B. Tendremos que calcular la longitud de ese arco aplicando la siguiente fórmula:
Calcular el perímetro de un sector circular
En el caso de que queramos sacar el perímetro de todo el sector circular, debemos sumar a la longitud del arco 2 veces el radio, es decir:
Perímetro sector circular = longitud arco + 2r
Si lo expresamos de forma matemática, la fórmula para calcular el perímetro del sector circular es:
Ejercicios de sector circular
Para poner en práctica todo lo aprendido hasta ahora, vamos a hacer un ejercicio resuelto en el que nos piden calcular la superficie, longitud del arco y perímetro de un sector circular cuyo radio es 6cm y α=90º.
Empezaremos con el área ya que es la primera fórmula que hemos visto en la teoría:
Recuerda que las unidades de superficie van elevadas al cuadrado. Si no lo dejas indicado, puede que te resten puntos en la calificación del ejercicio.
A continuación calcularemos el arco del sector circular:
Con el arco ya calculado, el perímetro se obtiene de forma muy sencilla ya que sólo tenemos que sumar dos veces la longitud del radio. El proceso completo para calcularlo sería el que tienes a continuación:
Si te ha quedado alguna duda o tienes algún problema a la hora de resolver algún ejercicio, déjanos un comentario y te ayudaremos a solucionarlo.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.